Trapez i okręgi.
Mila: Zadanie dla Saizou.
W trapez równoramienny, którego obwód wynosi 16, a długość przekątnej 5, wpisano okrąg.
Oblicz długość promienia tego okręgu, długość promienia opisanego na tym trapezie oraz pole
tego trapezu.
Powodzenia, sprawdzę o 22.
30 lip 18:32
rumpek: Na szybko to promień okręgu wpisanego: 1,5; Pole: 12; Promień okręgu opisanego: 10/3

30 lip 18:53
Eta:
Zgadza się co do "joty"

30 lip 19:35
rumpek: 
30 lip 19:44
rumpek: mimo odpowiedzi

to zadanie wciąż jest dla
Saizou 
30 lip 19:44
Eta:
Ma się rozumieć!

30 lip 19:47
Eta:
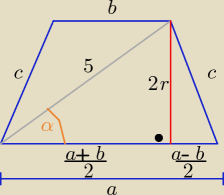
Myślę,że rys. pomoże

30 lip 19:56
rumpek: ale on wiedział jak zrobić

30 lip 19:57
rumpek: myślę, że wskazówka: c + c = a + b ⇒ 2c = a + b pomoże

30 lip 19:57
Eta:
Skąd to wiesz?

30 lip 19:58
rumpek: w trapez wpisany jest okrąg

30 lip 19:58
Eta:


I zaraz będzie rozwiązane !
30 lip 19:58
rumpek: to da się inne

ale
Mila może się obrazić

30 lip 19:59
Eta:
No wpisany okrąg!

h= 2r
30 lip 20:00
rumpek: | | a | |
zgadza się  opisany na okręgu czyli 2R = |
| |
| | sinα | |
30 lip 20:01
Eta:
Ejj tam
 Mila
Mila nam wybaczy ......... za

(rodzaj korupcji

30 lip 20:01
rumpek: | | c | |
w tym przypadku: 2R = |
| |
| | sinα | |
30 lip 20:01
30 lip 20:02
rumpek: byłem szybszy

30 lip 20:02
Eta:

30 lip 20:03
rumpek: myślę, że
Mila wybaczy za rodzaj:



30 lip 20:04
Krzychu: | a+b | |
| ? skąd to się bierze? |
| 2 | |
30 lip 20:04
rumpek: z atmosfery

30 lip 20:05
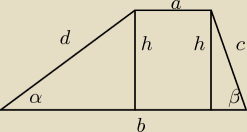
rumpek:
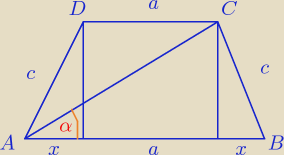
Taki rysunek też może być

a + b = c + c ⇒ 2c = a + b, gdzie b = a + 2x
16 = a + b + 2c ⇒ 4c = 16 ⇒ c = 4
a + b = 8
a + a + 2x = 8
2a + 2x = 8
a + x = 4
30 lip 20:08
Krzychu: a tak naprawdę?
30 lip 20:09
Eta:
@
Krzychu
| | a+b | | a−b | |
|
| + |
| = .......... = a |
| | 2 | | 2 | |
30 lip 20:11
rumpek: 
30 lip 20:11
Eta:
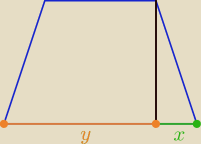
| | a−b | | a+b | |
x= |
| to: y= |
| , bo x+y= a |
| | 2 | | 2 | |
30 lip 20:14
Eta:
 rumpek
rumpek 
30 lip 20:14
rumpek: mój sposób też poprawny

30 lip 20:16
Krzychu:
2
2+{2r
2}=5
2
4+4r
2=25
Dobrze?
30 lip 20:18
Krzychu: tam miało być (2r)2
30 lip 20:18
rumpek: herezja matematyczna

30 lip 20:21
rumpek: podałem wyniki w 2 poście

30 lip 20:21
rumpek: | | 8 | |
i od kiedy to |
| = 2  |
| | 2 | |
30 lip 20:22
rumpek: poza tym to zadanie dla Saizou

30 lip 20:22
Krzychu: pomyliły mi sie.
30 lip 20:22
Saizou : to ja poczekam na Milę od 22 i da mi inne zadanie
30 lip 20:26
rumpek: co za proste

?
30 lip 20:27
Eta:
| | 8 | |
Może po wejściu do Unii |
| = 2  |
| | 2 | |
30 lip 20:28
30 lip 20:29
rumpek: 
30 lip 20:29
Eta:
Masz c i 2r to z tw, Pitagorasa
30 lip 20:30
rumpek: | | a − b | |
a po co ci liczyć |
| , za rok maturka krzysiu  ? |
| | 2 | |
30 lip 20:30
Eta:
rumpek ..... nie osłabiaj mnie

30 lip 20:30
Eta:
No, bo tak chciał

30 lip 20:31
rumpek: czym Cię
Eto osłabiam

30 lip 20:33
30 lip 20:34
rumpek: 

30 lip 20:36
rumpek: po prostu pocieszna ze mnie osóbka

30 lip 20:37
rumpek: lub dla naszego prezydenta os
Ubka

30 lip 20:37
Saizou : to się biorę za to zadanie
30 lip 20:37
Eta:
Lubię ludzi z poczuciem humoru (
chumoru dla ... dęta

30 lip 20:39
Krzychu: ja pierwszy raz zobaczę prezydenta już w czwartek

. Może mu dłoń uścisne.
16=9+x
2
x=
√7 ?
30 lip 20:41
rumpek: no i znowu "wafla" strzele: "

"
30 lip 20:41
rumpek: to poproś go aby napisał Twój nick forumowy

będzie "Krzychu" czy "Kżyhu"

30 lip 20:41
Eta:
| | a−b | |
@Krzychu , ale o |
| nie pytają, i to jest zbędne obliczenie  |
| | 2 | |
30 lip 20:43
Eta:

30 lip 20:43
Krzychu: no ale ja chce tą część znać zeby wiedzieć ile ma całe a.
30 lip 20:44
Eta:
Do czego Ci potrzebne w tym zadaniu"a"? ........
30 lip 20:45
Dawit:
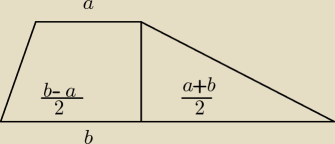
Eta to jest co narysowałem jest prawdą ? po zsumowaniu da b

30 lip 20:47
Eta:
A jak myślisz?

30 lip 20:50
Krzychu: | | a+b | |
ok mam, pomyliłem się w liczeniu i chciałem to..Dzieki. Nie wpadłbym na to |
| i |
| | 2 | |
30 lip 20:51
30 lip 20:51
Dawit: mysle że tak ale nie potrafię sobie tego wyobrazić
30 lip 20:51
Bartek : Widzę, że miło się tu wszystkim gaworzy, ale osobiście miałem nadzieję, że otrzymam pomoc także
w przypadku mojego zadania. A ciebie Eta poprosiłem,bo mam wrażenie że jesteś tu największym
matematycznym guru...
Jeszcze raz podaje link: chodzi oczywiście o zadanie na samej górze. Treść oczywiście już
rozumiem, ale jak to sensownie rozwiązać to nie wiem.
https://matematykaszkolna.pl/forum/151842.html
30 lip 20:56
Bartek : Tzn. już wiem że b=4, ale jak to matematycznie wyliczyć..
30 lip 20:57
Dawit: Aha jednak to nie prawda

To nie wiem podobnie jak Krzysiek skąd tam się to wzieło

30 lip 20:59
Krzychu: Dawit w Twoim to bzdura, bo Ty nie masz trapezu równoramiennego. I jak sobie poprowadzisz
wysokości, to bedziesz miał dwa trójkaty o róznych podstawach.
Ja wiem jak to jest w moim trapezie, ale nie wpadłbym na to na maturze. Teraz w razie co już
będe chyba wiedział.
Pole wyszło mi 12
30 lip 21:02
Eta:
@
Bartek i tu Cię zaskoczę

............. nie pamiętam już tego

Musiałabym odświeżać tę wiedzę , poczekaj na
Milę 
30 lip 21:03
Eta:
No to
Krzychu już C i wyjaśnił ........ tylko w
równoramiennym
A tak przy okazji:
| | a−b | |
Ciekawe to,że w szkole uczą was,że x= |
| |
| | 2 | |
| | a+b | |
a czemu nie uczą,że y= |
| ......... a szkoda  |
| | 2 | |
30 lip 21:05
Dawit: u mnie w szkole w ogóle nie używaliśmy niewiadomych

30 lip 21:06
Krzychu: bo tego nie widać na oko

30 lip 21:08
Bartek : Poczekam,bo to jest wiedza istotna w informatyce i chodzi o to, że po prostu muszę nie tylko
takie rzeczy umieć. Ale okej,dzięki. Przynajmniej wiem już do kogo uderzyć.
A przy okazji: czy tu chodzi o dział systemów liczbowych czy o jakiś inny? Kurcz, może są
jakieś arytmetyczne własności, sposoby...to bym już sobie sam to wygooglał.
30 lip 21:09
Dawit: Krzychu już wiem skąd się to wzięło mogę ci wytłumaczuc

DDDDD
30 lip 21:11
Saizou : ja mam wyliczone, że
c=4
P
t=(16−2c)r=8r
30 lip 21:12
Saizou : jeszcze zostało mi do wyliczenia R
30 lip 21:29
Saizou : jak wyliczyć promień okręgu opisanego na trapezie

z/w
30 lip 21:36
rumpek: napisałem

30 lip 21:37
30 lip 21:37
rumpek: Twierdzenie sinusów

30 lip 21:40
rumpek: Eta jakie podsumowanie tematu machnęła

30 lip 21:41
Eta:

30 lip 21:45
Saizou : pole mam już i promień okręgu wpisanego
30 lip 21:51
Eta:
Teraz popatrz na rys. mój lub
rumpka
Okrąg opisan na trójkącie ABC jest też opisanym na tym trapezie
to z tw. sinusów dla ΔABC
R=.....
30 lip 21:55
Krzychu: rumpek wiesz moze ile kosztuje Delta, ten miesięcznik

?
30 lip 22:00
30 lip 22:01
rumpek: 4zł, bardzo dobre czasopismo, polecam

30 lip 22:03
Saizou : to może jeszcze jedno zadanko tylko nie typu wykaż, udowodnij itp.
30 lip 22:08
Krzychu: Dany jest trójkąt prostokątny ABC o kącie prostym przy wierzchołku C. Promień okręgu wpisanego
jest równy r. Wykaż, że pole trójkąta ABC pomniejszone o r2 jest równe r*|AB|.
30 lip 22:12
rumpek: Krzysiu umiesz ty czytać

?
30 lip 22:13
Saizou : znowu mam coś wykazać

Jestem na NIE
30 lip 22:16
Eta:
zad 1/ Wyznacz liczbę dwucyfrową taką ,że suma jej cyfr jest równa 12
a suma kwadratów jej cyfr jest równa 80
30 lip 22:17
Krzychu: Nie zauważyłem tego
nie 
30 lip 22:17
rumpek: to masz takie łatwe: "W trapezie, kąty α i β są przy dłuższej podstawie. Mając podaną wysokość
h oblicz P tej figury. [można wpisać w ten trapez okrąg]

"
30 lip 22:18
30 lip 22:19
Saizou : a,b∊{0,1,2...9} a≠0
10a+b liczba dwucyfrowa
a+b=12→a=12−b
a
2+b
2=80
(12−b)
2+b
2=80
144−24b+b
2+b
2=80
2b
2−24b+64=0
b
2−12b+32=0
Δ=144−128=16
√Δ=4
zatem mamy
a=12−4=8 b=4 zatem liczbę 84
a=12−8=4 b=12 zatem liczbę 48
30 lip 22:28
Eta:


30 lip 22:28
Saizou :
| | 2P | | r(a+b+c+d) | |
r= |
| → |
| =P
|
| | a+b+c+d | | 2 | |
a+b=c+d
zatem
30 lip 22:40
Mila: Saizou:
Uwagi:
Nie zaznaczyłeś kąta α,
Nie zauważyłeś, że 2c=16:2
Wyniki dobre.

Może Krzychu napisze pełne rozwiązanie. Zobacz wskazówki Rumpka i Ety.
30 lip 22:42
Saizou : nie zaznaczyłem kąta alfa bo sugerowałem się w ten czas rysunkiem rumpka
30 lip 22:44
Saizou : | | 16 | |
a że 2c= |
| nie trzeba było zauważyć  |
| | 2 | |
30 lip 22:44
Krzychu: czyżby chodziło o to, że można wpisać okrąg tylko w trapez równoramienny?
30 lip 22:53
Saizou : to co ostatnie zadanie na dziś? może być trochę trudniejsze, tylko nie dowód geometryczny
30 lip 22:56
Karmik: Delta − co to za miesięcznik co się w nim dzieje ?
30 lip 22:56
Mila: Krzychu, nie tylko, ale jesli mozna wpisać to sumy przeciwległych boków są równe.
30 lip 22:57
rumpek: typowo matematyczno−fizyczno−informatyczno−astronomiczny, dowody, czasami całki równania
różniczkowe

itp.
30 lip 23:07
rumpek: same fajne rzeczy


30 lip 23:07
Krzychu: Mila, a o co jeszcze

?
30 lip 23:07
Eta:
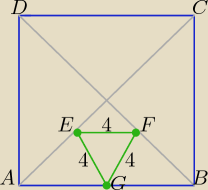
Wyznaczyć pole kwadratu ABCD
Zadanie dla
Saizou i
Krzycha 
30 lip 23:23
nikt: 64 + 32
√3 
30 lip 23:26
rumpek: rasizm normalnie

30 lip 23:27
nikt: dyskryminują grubasków

30 lip 23:28
rumpek: bardziej chodziło mi o zadaniowy

30 lip 23:29
Eta:
Bardziej elegancki wynik: 32(2+
√3) [j
2]

30 lip 23:30
rumpek: potwierdzam

30 lip 23:31
Eta:

30 lip 23:32
Krzychu: za mało danych w tym zadaniu

30 lip 23:41
Krzychu: powiedzcie co mam zauważyć/na co zwrócić uwagę

.
30 lip 23:50
Krzychu: albo nie, na razie zauwazylem ze da sie katy obliczyc.
30 lip 23:52
31 lip 00:05
rumpek: taki trójkąt nie istnieje

31 lip 00:08
rumpek: suma miar kątów w trójkącie to 180
o, u ciebie nie ma tylu

31 lip 00:08
rumpek: ajć sorki

nie zauważyłem, gdzie oznaczyłeś β

zwracam honor

31 lip 00:09
rumpek: mimo to wynik niepoprawny

31 lip 00:10
Krzychu: ale α i c są dobrze?
31 lip 00:14
Mila: Krzychu, oblicz to, co się da, wysokość w Δ równobocznym...OF, ...
31 lip 00:16
Krzychu: h=2√3
31 lip 00:24
Krzychu: te kąty α oraz c są ok?
Nie wiem co z tej wysokości.
31 lip 00:31
Eta:
A może widzisz trójkąty podobne ?

31 lip 00:32
rumpek:
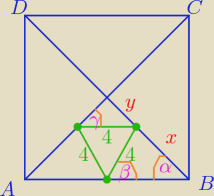
Oznaczenia: α = 45
o, β = 60
o, γ = 45
o
Liczę x:
4
√3 =
√2x / *
√2
4
√6 = 2x / : 2
x = 2√6
Liczę y:
y = 2√2
a
√2 = 2 * (2
√2 + 2
√6)
a
√2 = 4
√2 + 4
√6 / *
√2
2a = 8 + 4
√12 / : 2
a = 4√3 + 4
P = a
2
P = (4
√3 + 4)
2 = 16 * 4 + 32
√3 + 16 = 64 + 32
√3 =
32(2 + √3) [j2]
koniec

31 lip 00:32
rumpek: Rozwiązane sposobem Krzycha

31 lip 00:33
Kejt: i zepsuł..
31 lip 00:33
rumpek: czemu

można zrobić innymi sposobami

ja zrobiłem podobieństwem na karteczce

31 lip 00:34
Kejt: ale jak się ma już jedno rozwiązanie to potem żadna frajda

31 lip 00:37
Krzychu: te wielkie 4 trojkaty sa podobne i dwa powstałe po bokach zielonego.
na pewno nie jest pdoobny zielony do tego nad nim malutkiego. Bo w malutkim jest kat prosty.
31 lip 00:39
Eta:
a=2x −− dł boku kwadratu, h
Δ=2
√3
Krzychu teraz dokończ ........
31 lip 00:41
rumpek:
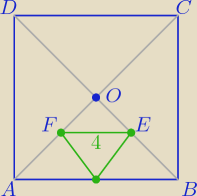
Trójkąt △OEF jest kwadratowy więc odcinek |OE| = 2
√2. Wysokość tego trójkąta będzie wówczas
wynosiła: h = 2. Wysokość trójkąta równobocznego wynosi h
1 = 2
√3. Sumujemy te dwie
| | a | |
wysokości: |
| = 2 + 2 √3 / * 2 ⇒ a = 4 √3 + 4. P = (4 √3 + 4) 2 = ...  |
| | 2 | |
31 lip 00:44
Eta:
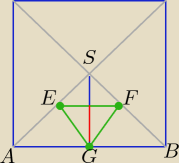
ΔABS ~ ΔEFS
31 lip 00:45
Eta:

31 lip 00:46
rumpek: Zgadza się

31 lip 00:47
Eta:
"trójkąt jest
kwadratowy " ?


(nie znam takich

31 lip 00:48
rumpek: ja to tak nazywam

czyli: trójkąt równoramienny mający kąt prosty w wierzchołku, jest na to
fachowa nazwa tylko mi z głowy teraz wyleciała

31 lip 00:52
Eta:
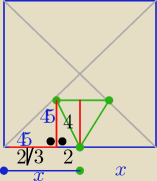
Można też tak:
a=2x= 4+4
√3
P= (4+4
√3)
2
31 lip 00:55
Eta:

31 lip 00:58
31 lip 00:59
Krzychu: trzeba sie nauczyć na pamięć kroki, potem powoli to zrozumieć.
31 lip 01:01
Mila: Teraz zauważyłam, że Rumpek też tak rozwiązał.( no właśnie ten trójkącik to połowa kwadracika)
Patrzyłam na problemy Krzycha.
31 lip 01:05
Eta:
Pora spać

bo muszę
"raniutko" wstać (tzn, o 10
oo 
Dobranoc Wszystkim

31 lip 01:05
Krzychu: dobranoc i dzięki.

31 lip 01:07
Eta:
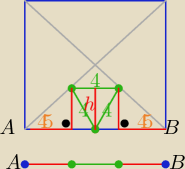
Najprostszy sposób

|AB|= 2
√3+4+2
√3= 4+4
√3
31 lip 18:13
rumpek: rozwiązań tyle co grzybów po deszczu


31 lip 18:15
31 lip 18:27
Eta:

31 lip 18:43



 to zadanie wciąż jest dla Saizou
to zadanie wciąż jest dla Saizou 

 Myślę,że rys. pomoże
Myślę,że rys. pomoże 





 I zaraz będzie rozwiązane !
I zaraz będzie rozwiązane !
 ale Mila może się obrazić
ale Mila może się obrazić 
 h= 2r
h= 2r
 opisany na okręgu czyli 2R =
opisany na okręgu czyli 2R = 
 Mila nam wybaczy ......... za
Mila nam wybaczy ......... za  (rodzaj korupcji
(rodzaj korupcji 








 Taki rysunek też może być
Taki rysunek też może być  a + b = c + c ⇒ 2c = a + b, gdzie b = a + 2x
16 = a + b + 2c ⇒ 4c = 16 ⇒ c = 4
a + b = 8
a + a + 2x = 8
2a + 2x = 8
a + x = 4
a + b = c + c ⇒ 2c = a + b, gdzie b = a + 2x
16 = a + b + 2c ⇒ 4c = 16 ⇒ c = 4
a + b = 8
a + a + 2x = 8
2a + 2x = 8
a + x = 4


 rumpek
rumpek 





 ?
?


 ?
?











 . Może mu dłoń uścisne.
. Może mu dłoń uścisne.
 "
"
 będzie "Krzychu" czy "Kżyhu"
będzie "Krzychu" czy "Kżyhu"


 Eta to jest co narysowałem jest prawdą ? po zsumowaniu da b
Eta to jest co narysowałem jest prawdą ? po zsumowaniu da b 

 To nie wiem podobnie jak Krzysiek skąd tam się to wzieło
To nie wiem podobnie jak Krzysiek skąd tam się to wzieło 
 ............. nie pamiętam już tego
............. nie pamiętam już tego  Musiałabym odświeżać tę wiedzę , poczekaj na Milę
Musiałabym odświeżać tę wiedzę , poczekaj na Milę 



 DDDDD
DDDDD
 z/w
z/w




 ?
?

 ?
?
 Jestem na NIE
Jestem na NIE

 "
"



 Może Krzychu napisze pełne rozwiązanie. Zobacz wskazówki Rumpka i Ety.
Może Krzychu napisze pełne rozwiązanie. Zobacz wskazówki Rumpka i Ety.

 itp.
itp.


 ?
?
 Wyznaczyć pole kwadratu ABCD
Zadanie dla Saizou i Krzycha
Wyznaczyć pole kwadratu ABCD
Zadanie dla Saizou i Krzycha 








 .
.
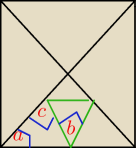 α=45o
β=60o
c=60o
czyli kopia tego: https://matematykaszkolna.pl/strona/551.html
a=4p{6]
a to do kwadratu daje 96
α=45o
β=60o
c=60o
czyli kopia tego: https://matematykaszkolna.pl/strona/551.html
a=4p{6]
a to do kwadratu daje 96


 nie zauważyłem, gdzie oznaczyłeś β
nie zauważyłem, gdzie oznaczyłeś β  zwracam honor
zwracam honor 


 Oznaczenia: α = 45o, β = 60o, γ = 45o
Liczę x:
Oznaczenia: α = 45o, β = 60o, γ = 45o
Liczę x:


 można zrobić innymi sposobami
można zrobić innymi sposobami  ja zrobiłem podobieństwem na karteczce
ja zrobiłem podobieństwem na karteczce 

 Trójkąt △OEF jest kwadratowy więc odcinek |OE| = 2√2. Wysokość tego trójkąta będzie wówczas
wynosiła: h = 2. Wysokość trójkąta równobocznego wynosi h1 = 2√3. Sumujemy te dwie
Trójkąt △OEF jest kwadratowy więc odcinek |OE| = 2√2. Wysokość tego trójkąta będzie wówczas
wynosiła: h = 2. Wysokość trójkąta równobocznego wynosi h1 = 2√3. Sumujemy te dwie

 ΔABS ~ ΔEFS
ΔABS ~ ΔEFS



 (nie znam takich
(nie znam takich
 czyli: trójkąt równoramienny mający kąt prosty w wierzchołku, jest na to
fachowa nazwa tylko mi z głowy teraz wyleciała
czyli: trójkąt równoramienny mający kąt prosty w wierzchołku, jest na to
fachowa nazwa tylko mi z głowy teraz wyleciała 
 Można też tak:
a=2x= 4+4√3
P= (4+4√3)2
Można też tak:
a=2x= 4+4√3
P= (4+4√3)2




 bo muszę "raniutko" wstać (tzn, o 10oo
bo muszę "raniutko" wstać (tzn, o 10oo  Dobranoc Wszystkim
Dobranoc Wszystkim 

 Najprostszy sposób
Najprostszy sposób |AB|= 2√3+4+2√3= 4+4√3
|AB|= 2√3+4+2√3= 4+4√3





