Bogdan:
Dobrze, to wykres a.
Jeśli do wzoru funkcji można wstawić każdą liczbę, np. do wzoru f(x) = 2x = 3, to
dziedziną jest zbiór liczb rzeczywistych, D
f : x € R,
| | 2 | |
a jeśli nie, np. do wzoru funkcji g(x) = |
| nie można wstawić liczby 3, bo |
| | x−3 | |
wtedy w mianowniku pojawi się zero, wtedy dziedziną jest zbiór liczb rzeczywistych
oprócz 3, D
g: x € R \ {3}.
Przeciwdziedzinę tworzą wartości funkcji, w tym przypadku D
−1: y € R.
Trzeba dodać, że powinno się raczej określać zbiór wartości funkcji, a nie
przeciwdziedzinę.
Miejsce zerowe to ta wartość argumentu funkcji, dla której wartość funkcji
jest równa zero. Na wykresie to miejsce przecięcia wykresu osi x.
Monotoniczność określa przedziały, w których funkcja jest rosnąca, malejąca.
Dla funkcji liniowej f(x) = ax + b jeśli a > 0 to funkcja jest rosnąca, jeśli a < 0
to funkcja jest malejąca, a jeśli a = 0 to funkcja jest stała.
Bogdan:
A może chodzi Ci o funkcję f(x) = 5
x, a nie o f(x) = 5x.
Jeśli tak, to kliknij tu
187.
 o co chodzi
o co chodzi
 !
!

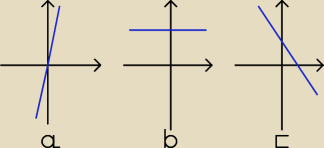 Który z wykresów: a, b, czy c odpowiada funkcji f(x) = 5x ?
Który z wykresów: a, b, czy c odpowiada funkcji f(x) = 5x ?

