; /
KASIA. : hej ; ]
wytłumaczy mi ktoś jak to się robi ? ; ]
Wyznacz równanie osi symetrii wykresu i zbiór wartości funkcji:
y = 2(x−3)2 +5
2 gru 21:26
2 gru 21:30
KASIA. : czyli będzie :
p=x=3
q=y=5
a zbiór wartości to trzeba wyliczyc p i q ?
2 gru 21:43
sushi_ gg6397228:
kliknij na drugi link−−> podali ZW jak ma wygladac
x=3 os symetrii
p=3
q=5
2 gru 21:52
KASIA. : czyli mam zapisać jako oś symetrii tylko x=3, tak ?
2 gru 21:53
sushi_ gg6397228:
tak os symetrii x= 3 bo przeciez tylko kreska pionowa dzieli parabole na dwa takie same "
obrazki" jak kreska pionowa na twarzy, dzieli ja na dwie takie same połówki
2 gru 21:58
KASIA. : ok a do zbioru muszę wyliczyć tylko q ?
czyli am być:
Δ=12
2−4*2*(−13) = 144+104=248
z.w <−31;+
∞)
2 gru 22:03
sushi_ gg6397228:
przeciez p, q masz juz podane w zadaniu−−> podalas ze o 21.43
2 gru 22:05
KASIA. : aha
czyli z.w <5;+
∞) ?
2 gru 22:06
sushi_ gg6397228:
bingo
2 gru 22:09
KASIA. : ok
bo mam parę takich przykładów..
możesz mi je sprawdzić ?
1. y=5(x+4)
2+1
x=−4
z.w <1;
∞)
2. (x−2)
2−7
x=−2
z.w <−7;
∞)
3.y=−2(x−6)
2+4
x=6
z.w (−
∞;4>
4. −4(x+1)
2−2
x=−1
z.w (−
∞;−2>
5. −(x−5)
2−4
x=5
z.w (−
∞;−4>
2 gru 22:18
sushi_ gg6397228:
1 ok
2. x=... do poprawki
3. ok
4. ok
5. ok
2 gru 22:21
KASIA. : 2. x=2
2 gru 22:23
KASIA. : y=2(x−3)2
x=3
a jak wtedy z.w ? zbiór pusty ?
2 gru 22:24
sushi_ gg6397228:
y=2(x−3)2 + 0
2 gru 22:27
KASIA. : czyli z.w <0;+∞) ?
2 gru 22:29
sushi_ gg6397228:
przeciez mamy parabolke, wiec zbior pusty to byla czysta HEREZJA
ok
2 gru 22:32
KASIA. : ok .
a ten ?
y=−5(x+2)
2
x= −2
z.w (−
∞;0>
2 gru 22:33
sushi_ gg6397228: ok
2 gru 22:34
KASIA. : a jak jest tak to ja mam to rozkładać czy co ?
y= x2+1
2 gru 22:35
KASIA. : sorry, ma być y= x2−1
2 gru 22:36
sushi_ gg6397228:
y= (x
−0)
2 − 1 i juz po problemie
2 gru 22:44
KASIA. : aha ..
czyli x=0
z.w <−1;∞)
2 gru 22:46
sushi_ gg6397228: bingo
2 gru 22:46
KASIA. : jeszcze mam takich 6 przykładów .. ; /
też je trzeba jakoś rozkładać czy coś ? ; /
9. 3x2+5
10. y= −2x2−6
11. y=−x2+4
12. x2−4x−1
13. 4x2+3x+2
14. y=−3x2−4x+1
2 gru 22:48
KASIA. : 9. y= (3x+0)
2+5
x=0
z.w <5;
∞)
2 gru 22:49
2 gru 22:50
sushi_ gg6397228:
9. y= 3(x+0)2 +5 zawsze musi byc y= a(x−p)2+ q
2 gru 22:52
sushi_ gg6397228:
policzone OK, zapis taki jak u mnie
2 gru 22:52
KASIA. : czyli
10. y=−2(x+0)2−6
x=0
z.w (−∞;−6>
11. y =−(x=0)2+4
x=0
z.w(−∞;4>
2 gru 22:54
sushi_ gg6397228:
10 i 11 ok
2 gru 22:56
KASIA. : 12. p=2
q=−5
czyli x=2
z.w <−5;∞)
2 gru 22:58
sushi_ gg6397228:
12ok
2 gru 23:01
2 gru 23:05
sushi_ gg6397228:
13 ok
14 ok
2 gru 23:07
KASIA. : ok a możesz i jeszcze powiedzieć czy to mam dobrze ?
Podaj równanie asymptot wykresu funkcji
as. pionowa x=3
as. pozioma y=1
2 gru 23:22
sushi_ gg6397228:
ok
2 gru 23:26
KASIA. : a jak zrobić te?
1. f(x) =3x
2. f(x) =3x−2
3.f(x) =3x+4
4. f(x) =3x−2+4
5. f(x) =−3x
6. f(x) =−3x+4
2 gru 23:29
sushi_ gg6397228:
g(x)= 3x−p +q gdzie p,q to przesuniecia, takie same jak w paraboli
2 gru 23:32
sushi_ gg6397228:
h(x)= − 3x −−> wykres caly idzie na dół (odbicie wzgledem osi OX)
2 gru 23:33
KASIA. : czyli w 1 będzie
x=0
y=0 ?
2 gru 23:35
sushi_ gg6397228:
nie napisalas, co chcesz policzyc
2 gru 23:39
KASIA. : 2. x=2
y=0
3. x=0
y=4
4.x=2
y=4
5. x=0
y=0
6.x=0
y=4
2 gru 23:41
2 gru 23:41
KASIA. : 2.
3x −−−T[2,0]−−−−> 3x−2
o to chodzi ?
2 gru 23:45
sushi_ gg6397228:
to tylko podalem przesuniecia
nie wiem co masz policzyc−−> bo podalas suche przyklady
2 gru 23:46
KASIA. : no takie mam zrobić
2 gru 23:47
sushi_ gg6397228:
5 i 6 to najpierw jest odbicie wzgledem osi OX a potem przesuniecie
2 gru 23:49
KASIA. : czyli jak ? ; /
2 gru 23:51
sushi_ gg6397228:
2,3,4 ok
2 gru 23:52
sushi_ gg6397228:
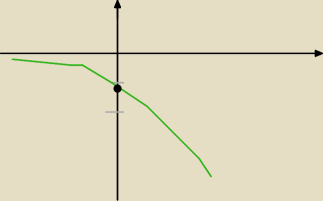
to masz do zad 5
do zad 6 to ten rysunek przesun o 4 do gory
2 gru 23:55
KASIA. : ta kropka to ile to jest ?
2 gru 23:57
sushi_ gg6397228:
tyle co linku, tylko z minusem
−1
3 gru 00:00
KASIA. : czyli jak mam to zapisać?
5. f(x) = 3x −−−ox−−−>−3x
3 gru 00:04
sushi_ gg6397228:
np: symetria wzgledem osi OX
3 gru 00:05
KASIA. : i wtedy x i y są równe 0 oby dwie ?
3 gru 00:06
sushi_ gg6397228:
nie ma zadnego przesuniecia
jest p , q, a nie jakies tam x,y
3 gru 00:10
KASIA. : ale mi o asymptoty chodzi... ; /
to co w końcu mam zapisać ?
3 gru 00:11
sushi_ gg6397228:
to asymptota to tylko jest pozioma
zobacz na rysunek w linku
y=q
3 gru 00:13
KASIA. : czyli
x=0
y=−1
3 gru 00:15
sushi_ gg6397228:
1. f(x) =3x asymp. y=0
2. f(x) =3x−2 asymp y=0
3.f(x) =3x+4 asym y=4
4. f(x) =3x−2+4 asym y=4
5. f(x) =−3x asym y=0
6. f(x) =−3x+4 asym y=4
3 gru 00:15
KASIA. : a pionowej nie ma ?
3 gru 00:17
KASIA. : w żadnej ?
3 gru 00:18
sushi_ gg6397228:
a ogladalas rysunek z linku
3 gru 00:18
KASIA. : tak
3 gru 00:19
sushi_ gg6397228:
to widziesz ze funkcja jest rosnaca i leci sobie do nieba, wiec nie ma zadnej kreski pionowej,
co by jej przeszkodzila w tym zamiarze
3 gru 00:20
KASIA. : to po co ja w 6 miałam przesuwać o 4 jednostki do góry ? nie rozumiem ..
3 gru 00:20
KASIA. : czyli w żadnym przykładzie nie ma as.pionowej same poziome ?
3 gru 00:22
sushi_ gg6397228:
bo w zad 5 masz wykres pod osia, a w zad 6 ten sam wykres przesuniety o 4 do gory,
nie podalas co chcesz liczyc Z.W. czy co innego , wiec przestawilem jak by to wygladalo
3 gru 00:22
sushi_ gg6397228:
f. wykladniczama tylko pozioma
f(x)= ax−p +q asymp pozioma y= q
3 gru 00:23
KASIA. : no w zdaniu jest że mam podać równanie asymptot wykresu funkcji
3 gru 00:24
sushi_ gg6397228:
wiec je podalem o 00.15 −−> kropka
3 gru 00:25
KASIA. : ok.
dobra
dzięki z pomoc ; ]
3 gru 00:26
sushi_ gg6397228:
mam nadzieję, ze to nie byl stracony czas
3 gru 00:26
KASIA. : absolutnie nie. ; ] zapewniam, jeszcze raz dziękuje : )
3 gru 00:28