trapez pomocy agniecha: W trapezie ABCD (AB II DC) przekątne przecinają się w punkcie E. Pole trójkata AED jest równe 15cm,a pole trójkąta DEC wynosi 10cm. Oblicz: a) EC : AE b)pole trapezu ABCD

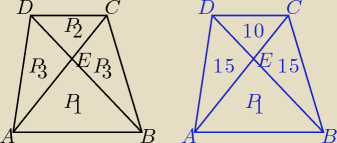
Bogdan: Podaję zależności potrzebne do rozwiązania zadania. Pole trapezu ABCD: P_ABCD = ( √P₁ + √P₂ )² = P₁ + P₂ + 2√ P₁*P₂ P₃ = √ P₁*P₂ ⇒ P₃² = P₁*P₂ Informacje o tych zależnościach znajdziesz tu 56604 i tu 35230. P₂ = 10, P₃ = 15, 15² = P₁*10 ⇒ P₁ = 22,5. Pole trapezu P_ABCD = 22,5 + 10 + 2*15 = ... Z podobieństwa trójkątów: CDE i ABE otrzymujemy (k − skala podobieństwa):

	P2		10		4		2
k2 =		=		=		⇒ k =
	P1		22,5		9		3

|EC|		2
	= k =
|AE|		3

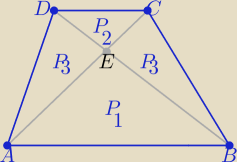Eta: Inny sposób: P₃=k*P₂ i P₁=k²*P₂ , k >0 −− skala podobieństwa ΔABE i DCE P(trapezu)= (k+1)²*P₂ W tym zadaniu:

	3		AE		3		EC		2
k*10=15 ⇒ k=		to		=		⇒		=
	2		EC		2		AE		3

	3		25
P(trapezu)=(		+1)2*10 =		*10= 62,5
	2		4