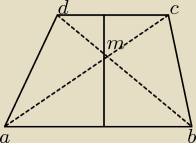
pole trapezu mała: przekątne trapezu abcd przecinają się w punkcie m. wysokosc trapezu ma długość 18. pole trójkata abm jest rowne 25, pole trojkata cdm jest rowne 16. oblicz pole trapezu

mała: nie wiem tylko jak wyprowadzic x... skad?

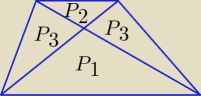
Bogdan: Podam gotowy wzór: Pole trapezu P = (√P₁ + √P₂)² P = P₁ + P₂ + 2√P₁*P₂ a także P = P₁ + P₂ + 2P₃ P₃ = √P₁*P₂

tim: Bogdanie, skąd ten wzór?

Bogdan: Wyprowadziłem ten wzór korzystając z podobieństwa trójkątów zawartych w trapezie. Już kiedyś był on na forum prezentowany, a nawet był wyprowadzany. Spróbuj tim sam go ustalić mając dane P₁ i P₂.

tim: A i jeszcze, czemu P3 i P4 są równe?

tim: Jakąś większą podpowiedź? Co do wyprowadzenia?

Bogdan:

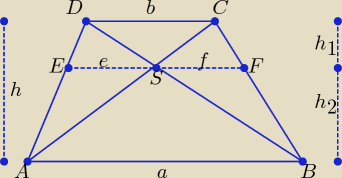
	e		h1
Z podobieństwa trójkątów ABD i ESD:		=
	a		h

	f		h1
Z podobieństwa trójkątów ABC i FSC:		=
	a		h

	e		f
Stąd		=		⇒ e = f
	a		a

h = h₁ + h₂ Pole trójkąta ASD:

	1		1		1		1
PASD =		*e*h1 +		*e*h2 =		e*(h1 + h2) =		eh
	2		2		2		2

Pole trójkąta ASD:

	1		1		1		1
PBSC =		*e*h1 +		*e*h2 =		e*(h1 + h2) =		eh
	2		2		2		2

Stąd P_ASD = P_BSC = P₃

tim: Dalej nie wiem. Jak znajdziesz chwilę, to wskazówkę następną.

Manon: rusz głową. Bogdan już za pierwszym razem podał ci rozwiązanie, właściwie musiałeś podstawić po wzoru to co miałeś.

dro: Mam potrzebę wiedzieć, skąd wziął się ten wzór, że P3 = √P1*P2 ?

Matematica: Przepraszam, czy pola trójkątów P3 są zawsze równe w każdym trapezie? A jesli tak, to czy wynikak to z właściwości ich kątów?