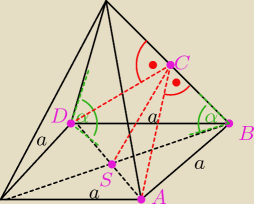
PROblem TOmek: Jest to ostrosłup prawidłowy czworokątny. Krawędź podstawy jest równa a, zaś krawędź boczna jest nachylona do podstawy pod kątem α. Ostrosłup przecięto płaszczyzną przechodzącą przez przekątną podstawy i równoległą do krawędzi bocznej. −−−−−−−−−−−−−−−− mam parę pytań: 1) Czy trójkąt SBC jest prostokątny? 2) ∡CSB=∡CBS=α jest prawdą, jeśli tak to występuje to w ostrosłupach prawidłowych?

Godzio: 1) Czy w poleceniu jest napisane że krawędzie boczne przecinają się pod kątem prostym 2) Skoro SC jest równoległa do krawędzi bocznej to tak

TOmek: czaje , danke

TOmek: ale oczywiście SBC jest to juz trójkąt prostokątny?

TOmek: NIE SBC tylko ABC literówka

rumpek: Co masz zrobić w tym zadaniu? Jakie polecenie ? Bo rozwiązałbym sobie to zadanie, fajne się wydaje.

TOmek: to ABC jest prostokątny czy nie? P_przekroju = a²/4cosα

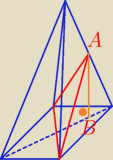
rumpek: Według mnie ABC nie jest trójkątem prostokątnym, tobie chodzi chyba o sytuacje jak kąt dwuścienny ma tam kąt prosty. W tym rysunku możesz puścić prostą prostopadłą do podstawy na rysunku u mnie to |AB| Czyli trzeba obliczyć pole przekroju? Zaraz się za to biore

TOmek: Godzio?

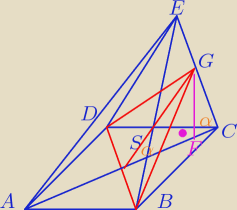
rumpek: Jakby cos Bozia nie dała mi talentu plastycznego, co widać Wiemy, że |AB| = |BC| = |CD| = |AD| = a Przekątna kwadratu to: a√2 czyli |AC| = |DB| = a√2 (rysunek nie wyszedł)

	a√2
Odcinek |CS| =
	2

I teraz kluczowy moment to co wyżej napisałem ten odcinek |AB| w górnym rysunku to krzywo

	a√2
wyszedł bo on dzieli tak jakby na pół |CS| czyli mamy
	4

Taka uwaga na odcinku |CE| punkt G jest po środku (wiem wiem koślawe rysunki − tak jak wyżej wspomniałem ten tak jakby rzut z punktu G na podstawę też powinien być na środku czyli

	a√2
		− ale o tym pisałem)
	4

To teraz korzystamy z https://matematykaszkolna.pl/strona/397.html

	1
Pole przekroju to: P =		a*h
	2

	a√2
a mamy bo to jest		a h zaraz się policzy z tych zależności
	2

	|FS|
cosα =
	|GS|

	a√2   4
cosα =
	|GS|

	a√2
|GS| =
	4cosα

No i teraz tak jak pisałem liczymy pole i otrzymujemy twój wynik:

	a√2   a√2 *   4cosα		2a2		a2
P =		=		=
	2		8cosα		4cosα

TOmek: rozwiązać to ja to potrafie tylko natrafiły mi sie pytania i nadal nie znam odpowiedzi.

rumpek: No to ci odpowiedziałem, że tam nie ma kąta prostego u ciebie tam na rysunku ABC nie wiem co ty tam widzisz. Trójkąt prostokątny jest tam gdzie ja u siebie na rysunku zaznaczyłem (troche krzywo ale żyjemy )

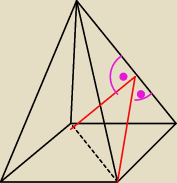
TOmek: Może tak zapytam, wiemy ,ze przekrój jest prostopadły do krawędzi bocznej, czyli występuje gdzieś tam kąt 90 stopnii, proszę niech ktoś mi teraz z tamtąd wydobędzie trójkąt prostokątny.

rumpek: Według mnie to co narysowałeś to jest kąt dwuścienny a nie o to chodzi w tym zadaniu (kierując się tymi kątami prostymi) lecz ja jeszcze stereometrii nie robiłem, wziąłem się za prawdopodobieństwo . Czyli to co narysowałeś to wygląda mi mniej więcej tak: https://matematykaszkolna.pl/strona/2522.html (kąt między sąsiednimi ścianami bocznymi). Lecz mogę się mylić jak każdy człowiek

TOmek: Dzięki rumpek, ja na razie tylko Ty podjąłes sie próby wyjasnienia mi tego. Moze dla niektórych z naszych eksertów jest to zbyt oczywiste i nie chce im sie tego pisac.

rumpek: https://matematykaszkolna.pl/forum/92332.html Tu jest to samo zadanie, i jak widzisz kąty podobne jak na moich rysunkach (moich niedokładnych rysunkach xD) Zauważ, że "równoległe" a nie prostopadłe.

TOmek: Równoległą, nie prostopadłą Aska zamiast Aśka powinni dać TOmek omg..

rumpek: Przecież Godzio ci napisał: "Czy w poleceniu jest napisane że krawędzie boczne przecinają się pod kątem prostym " ...

TOmek: w sumie sam ICSP miał wątpliwości co do tego zadnia ..

TOmek: dobra zaraz zadam pytanie pomijające kwestia tego zadania, bo mi sie w głowie zamerdało..

TOmek: http://img33.imageshack.us/img33/417/30905021.jpg zadanie 1. Od TOmka. Wykorzystująć oznaczenia A, B, C, D, wskąż trójkąty prostokątne. http://img33.imageshack.us/img33/417/30905021.jpg

rumpek: Nom 3 trójkąty Pan Jakub napisał tam

TOmek: DBC jest prostokątny. a ABC?

rumpek: zadania.info Tam jest twoja odpowiedź to samo zadanie z matury 2010 maj rozszerzona

TOmek: http://www.zadania.info/d42/6150522 wywnioskowałem ,ze trójką ABC nie jest prostokątny, tak?

rumpek: U ciebie ABC = ABE bodajże więc trójkąt prostokątny, oni z tego obliczali

rumpek: ABE − u nich rzecz jasna

TOmek: a jest pierwsza linijka napisane czarno na białym dzieki!

rumpek: Dlatego tam odesłałem

TOmek: ostatnie pytanie: http://img838.imageshack.us/img838/7412/da2t.jpg EBC∡=∡BEC ?

TOmek: chciałbym juz zakonczyc ten temat i podsumowac sobie go jakos, by na powtorzenie przed maturka pozostalo.

TOmek: Nie?

rumpek: A tobie skąd Ci się to wzięło ? P.S.: byłeś gdzieś na wakacjach?

TOmek: Dla pewnosci to napisałem. Wszystko juz jest jasne na szczescie... jestem spokojny.. Na wakacjach typowych nie byłem(bo pracowałem a teraz juz ligę w nogę zacząłem) tylko jakies wypady nad jezioro jednodniowe, imprezy itp. Mam nadzieje ,ze Ty nie napiszesz o wakacjach w Chorwacji 2 tygodniowych

rumpek: Nigdy nie byłem na wakacjach za granicą Tylko ograniczyłem się do tygodniowego popytu u babci a tak ze znajomymi i praca

rumpek: pobytu*

TOmek: praca, praca, praca, mam nadzieje ,ze dzieki tej nauce, kiedyś będzie sie zaliczało CHorwacyje, Grecyje itp ...

rumpek: hehe, w sumie jakie partie materiału zrobiłeś przez wakacje z matmy?

TOmek: Wszystko przerobiłem juz do wakacji (taki miałem plan). I od początku wakacji robie tak jak mi Godzio radził, zadania z róznych działow (średnio w 5 dni objeżdzam wszystkie działy). Lecz teraz trafiają sie juz takie hardcorowe zadanka, ze siedzi sie po 2h.. : ] Ale progress z amatora do stanu dzisiejszego jest niesamowity dla mnie, biorąc pod uwagę fakt ,ze ucze sie sam z uwzględnieniem oczywisice forum.

rumpek: Po wakacjach (w okresie szkolnym) będziesz coś kombinował dalej ? Czy zwalniasz tempo? Są inne przedmioty, też. Polski najgorszy, żeby zdać

Godzio: Najlepiej w roku szkolnym zasuwać zadania takie jak ludzie wsadzają na forum, przynajmniej ja tak robiłem, a w wolnym czasie rób sobie zadania ze zbiorów

rumpek: Witam Godzia coś dawno Cię nie widziałem na forum Jak tam wakacje − w tym roku wyjątkowo długie, cio ?

Godzio: Ano lecą i lecą, teraz byłem ze znajomymi na mazurach to pewnie dlatego mnie nie widziałeś, a zaraz znów wyjeżdżam, wracam i do pracy ehhh

TOmek: Po wakacjach na pewno tempo opadnie(ja nie tylko matme ucze sie w domu, lecz także ostro angola szlifuje). Pewnie od wrzesnia znajdzie sie tylko czas na jakies dwa maturalne zadanka na dzien z majmy. Polski −> tutaj zamilczmy, idę na farta, Oby 30%

TOmek: Fajne zadanko dzisiaj zrobiłem z geom. analitycznej. Punkty przecięcia paraboli y=x²−2x−8 z prostą 2x+y−1=0 sa końcami przekątnej rombu, którego pole jest równe 30. Oblicz współrzędne wierzchołków tego rombu. ODP: (3,−5) , (2,2), (−3,7), (−2,0) Ja masz czas to zrób sobie to zadanko, najlepiej na kartce, bo trudno sie robi geom. analityczną tutaj. Ciekawy jest sposób znalezenia 2 ostatnich wierzchołkow

Godzio: TOmek polskim się nie przejmuj, zobacz po mnie, jestem totalnym zerem humanistycznym a mimo to 76% nie wiem skąd, a lałem taką wodę że lepiej nie mówić

Godzio: Na maturze próbnej miałem to samo zadanie, tyle że wierzchołki już miałem dane, a zaraz mogę zrobić

rumpek: TOmek akurat geometria analityczna to mój jeden z ulubionych działów

Godzio: O ! To zadanie dla rumpka to nie ruszam

rumpek: Że tutaj na forum mam zrobić? − odpowiedź podałeś więc już nie będzie trudno. Zazwyczaj nie robię z wektorów tylko mniej więcej tak: podstawiamy y = x² − 2x − 8 (za y = −2x + 1 ) i mamy już punkty przekątnej czyli 2 punkty Mając te dwa punkty liczymy więc środkowy punkt przekątnej S, i możemy obliczyć prostą prostopadłą do tej prostej y = −2x + 1 przechodzącą przez punkt S Potem mając te dwa punkty liczymy długość odcinka podkładamy pod pole i otrzymujemy długość

	|AC| * |BD|
tamtej drugiej przekątnej. (P =		) Załóżmy, że te punkt na początku to A i C
	2

to teraz mamy B i D obliczyć, więc mając obliczoną |BD| dzielimy go na 2 i mamy |BS| i |SD|. No i teraz jak mamy to już przemyślane dalej robimy tylko: punkty D i B możemy oznaczyć (x,y) [za y wstawiamy tam tę prostą prostopadła przechodzącą przez punkt S wstawiamy wiem wiem zagmatwane] No i liczymy odległość punktu danego od prostej y = −2x + 1 o odległość obliczonej − |BS| lub |SD| otrzymamy wartość bezwzględną dwa rozwiązania i punkty dane Można było też zrobić sposobem na okręgu ale to inna bajka

rumpek: Nawet ostatnio nawet dowody geometryczne polubiłem