Izza: Czy ramiona paraboli nie mają iść w dół?

Jakub: Współczynnik przy x² to 1. Dla dodatniego współczynnika przy x² ramiona idą do góry.

Iza: mozesz mi wytłumaczyć kiedy mam zamalowywac na szaro na wykresie?

Jakub: Jest to napisane na stronie 93.

FKS_1939: dlaczego rozwiązaniem równania jest przedział (−2,5) a nie od (−∞,−2)v (5,+∞) ?

Jakub: Nierówność x²−3x−10<0 oznacza, że interesują mnie ujemne wartości funkcji kwadratowej x²−3x−10. Są one pod osią Ox i zaznaczyłem je na zielono na poprzedniej stronie. Te ujemne wartości są dla x∊(−2,5), dlatego to jest rozwiązanie nierówności.

FKS_1939: aha już rozumiem, wielkie dzięki

Kaloian : Hej Jakub tylko chcialem podziekowac dla wszystko... bo naprawde dobrze jest wyjasznione ! pozdrawiam

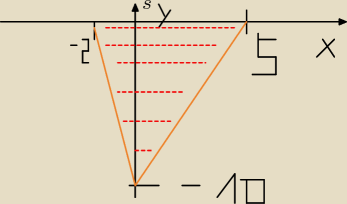
44: czyli wykres bedzie tak wygladal [ nie bierz pod uwage '' s '' obok "y" ]

aquagen: x1 jest chyba źle. 3 −7 / 2 = −4/2 czyli − 1/2 a nie −2

colorandcrazy: Jeżeli "a "jest dodatnie to ramiona idą w górę , a jak ujemne to w dół

Adam: dla mnie nie do zrozumienia jest to, czemu raz zamalowane mam na szaro w środku paraboli, a raz te rysunki rozchodzą się w dwie strony do nieskonczoności . od czego to zależne , nie mogę tego ogarnąć. Proszę o odpowiedź.

Adam: no arcy problem mi się zrobił na tydzień przed poprawką, godzinę myślę już nad tym o co chodzi z tym rozchodzeniem się wykresu, raz do środka, raz do nieskończoności, zapewne to banalne, a ja już tyle czasu przy tym tracę. Super.

Jakub: Zależy to od znaku nierówności. W tym przypadku masz x²−3x−10 < 0, czyli znak jest "<". Oznacza to, że x²−3x−10 ma być mniejsze od zera, czyli interesuje ciebie cześć paraboli POD osią x. Zaznaczyłem tą cześć na zielono. Ta zielona część jest dla x−ów od −2 do 5, dlatego zaznaczyłem ten szary przedział jako rozwiązanie nierówności. Gdybyś miał nierówność x²−3x−10 > 0 to by interesowała ciebie część wykresu NAD osią x, bo znak jest ">". Dla tej paraboli to są dwie części. Lewa część jest dla x−ów od −∞ do −2. Prawa część jest x−ów od 5 do ∞. Rozwiązaniem nierówności x²−3x−10 > 0 jest więc suma przedziałów (−∞,−2)u(5,∞).

Adam: czyli jeśli interesuje mnie zielona część pod spodem, to dla znaku < zawsze maluję na szaro do środka, a jeśli znak jest > to maluję w dwie strony? dziękuję w ogóle za szybką odpowiedź.

Jakub: Dla znaku "<" zaznaczasz na zielono, to co jest POD osią x. Dla tej zielonej części rysujesz szary przedział. Popatrz na ten rysunek 99. Znak jest "<", ale wcale nie rysujesz do środka, jak napisałeś. Są dwie zielone części i dla nich rysujesz dwa szare przedziały. Twoje myślenie, że dla "<" jest do środka, a dla ">" na zewnątrz jest więc błędne, gdy parabola ma ramiona do dołu. Lepiej myśleć tak jak napisałem. Znak "<" zaznaczasz część POD wykresem. Znak ">" zaznaczasz część NAD wykresem. Dla zaznaczonych części rysujesz szare przedziały, które są rozwiązaniami.

zieleniak: Wytłumaczcie mi kiedy trzeba zaznaczyć przedział w obrębie wykresu, a kiedy poza jego obrębem. Kompletnie tego nie rozumiem.

Jakub: Masz to opisane wyżej.

zieleniak: nie rozumiem tego kompletnie

Jakub: Próbuj, jak nie dziś to jutro zrozumiesz.

18: Rozwiazanie tego równania jest tutaj błędne. Powinien byc przedział od (−∞,−2) w sumie (5, +∞)

18: Rozwiazanie tego równania jest tutaj błędne. moim zdaniem Powinien byc przedział od (−∞,−2) w sumie (5, +∞)

Jakub: To weź jakąś liczbę ze swojego rozwiązania np. 6 podstaw za x do nierówności i zobacz, czy lewa strona wyjdzie mniejsza od zera.