Onim: tu jest blad z najmniejsza wartoscia funkcji
10 gru 19:20
Jakub: Jest dobrze.
13 gru 13:56
lysy wąż: dlaczego dobrze?
18 kwi 16:20
Jakub: A dlaczego nie? Ty mi napisz, gdzie widzisz błąd, a nie zadawaj dwuwyrazowe pytania.
18 kwi 22:38
ciekawski:
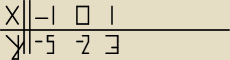
ten rysunek jest dla zobrazowania tego co chcę powiedzieć, gdybym nie wyrażał się jasno

a moje pytanie jest następujące: czy można zrobić taką tabelkę zamiast się rozpisywać tak jak w
przedstawionym zadaniu?
26 kwi 18:37
Jakub: Jak zaznaczysz te trzy punkty z tabelki w układzie współrzędnych to nie wiele widać. Nie
wiadomo czy wierzchołek jest w przedziale <−1,1> czy nie. Nawet jak się domyślisz, że jest to
nie bardzo widać na podstawie tylko trzech punktów gdzie. Ja wiem, że teraz patrzysz na swoją
tabelkę, na mój rysunek i stwierdzasz, że tabelką jest prościej. Jednak to tylko złudzenie, bo
już wiesz jak ta parabola wygląda.
Jakby coś z mojego rozwiązania było niezrozumiałe, to pytaj.
26 kwi 22:49
ciekawski: Odłóżmy układ równań, uznajmy, że nie wiemy jak wygląda, ani nie zamierzamy go rysować. I
teraz: skoro widać, że funkcja jest rosnąca (co wynika z tego, że x2 > x1 i y2 > y1) w
danym przedziale to czy naprawdę wierzchołek jest tak ważny do odczytania ymax i ymin?
Możesz mi wytłumaczyć dlaczego wierzchołek jest tak ważny i przez niego nie można skorzystać z
tej tabelki? Byłbym wdzięczny.
27 kwi 12:35
Jakub:
Najważniejsze w tego typu zadaniach jest ustalić, czy wierzchołek leży w przedziale czy nie.
Jeżeli wierzchołek funkcji leży w przedziale <−1,1> to najmniejsza wartość jest właśnie w tym
wierzchołku, a największą wartość sobie wybierasz z tych dwóch z krańców przedziału, czyli dla
x=−1 i x=2.
Gdy wierzchołek nie leży wewnątrz przedziału to sytuacja jest prosta. Liczysz wartości na
krańcach przedziału i z nich wybierasz najmniejszą i największą wartość przedziału.
Tak więc najważniejsze jest policzenie x
w na początku rozwiązywania i ustalenie czy należy do
<−1,1>.
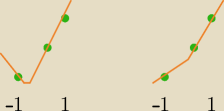
Zobacz na te rysunki. Wiem, że są kiepskie, ale wyobraź sobie, że to są fragmenty parabol. Na
lewym i prawym rysunku masz identycznie położone trzy zielone punkty. Na lewym rysunku
narysowałem parabolę, która ma najmniejszą wartość w wierzchołku. Na prawym rysunku
narysowałem parabolę (fragment jej prawego ramienia), która ma najmniejszą wartość w skrajnym
lewym zielonym punkcie.
Jak widzisz trzy jednakowe punkty i dwa różne najmniejsze wartości.
Nie możesz ustalić najmniejszej wartości na podstawie tylko trzech punktów, ponieważ nie jesteś
w stanie określić tylko na podstawie tych trzech punktów, czy wierzchołek leży w <−1,1> czy
nie, dopóki nie policzysz x
w.
Zauważ, że na lewym rysunku mimo, że punkty są rosnące, to funkcja nie jest rosnąca w całym
<−1,1>.
27 kwi 15:10
ciekawski: Tak, teraz już w pełni to zrozumiałem

Dziękuję za pomoc

28 kwi 09:56
monika: dlaczego najmniejszą wartością nie jest −6? Przecież W (−2,−6)
25 maj 18:29
Jakub: Wierzchołek W leży poza przedziałem <−1,1>, co widać na rysunku. Przeczytaj uważnie treść
zadania.
25 maj 19:55
Domi: mógłbys napisać jakos prościej?
2 sty 18:32
Domi: to my nie patrzymy na wirzchołek

a zawsze obliczamy p i q

2 sty 18:33
7uu: git majonze
12 mar 11:45
7uu: nie tylko z kanonicznej :0 pozdro 600
12 mar 11:46
Jakub: Zależy Domi czy ten wierzchołek leży w przedziale z tekstu zadania czy nie. Na poprzedniej
stronie wierzchołek leży poza przedziałem więc nie ma znaczenia.
12 mar 16:16
Worn: Ja zamiast rysowania wykresu funkcji i odczytywania z niej najmniejszej i największej wartości
jestem nauczony w następujący sposób:
y=x2+4x−2 <−1;1>
Liczymy ze wzoru funkcji wartość dla najmniejszego argumentu z przedziału, czyli dla −1
y=(−1)2+4*(−1)−2
y=1−4−2
y=−5
później dla największego argumentu z przedziału, czyli dla 1
y=12+4*1−2
y=1+4−2
y=3
Następnie liczymy współrzędną x wierzchołka paraboli ze wzoru xw=−b/2a
xw=−4/2*1
xw=−2
I teraz jeżeli xw ∊ <−1;1>, to obliczamy dla niego wartość, a jeżeli nie należy, to wyznaczamy
już wartości min i max
W tym przykładzie mamy ymin=−5 i ymax=3
31 maj 21:27
zbyszko: Mam pytanie. Nie odnośnie samego zadania, tylko poprawnego zapisu, np na maturze.
Ja to zadanie rozwiązałem w sposób następujący − najpierw sprawdziłem, czy funkcja jest
rosnąca, czy malejąca (zerkając na a), potem obliczyłem tylko p (żeby wiedzieć, czy mieści się
w przedziale), jeśli mieści obliczam również q (żeby znać najmniejszą/największą wartość, w
zależności od a). Jeśli wierzchołek mieści się w przedziale, to najmniejsza/największa wartość
poza nim to jeden z punktów końcowych. Jeśli nie, to oba punkty końcowe stanowią najmniejszą i
największą wartość. Wiem, to wszystko jest oczywiste...
Ale ja wszystkie obliczenia robię w trzech działaniach, od razu podaję odpowiedź. Czy to błąd?
Czy na maturze trzeba wykonywać opisy wykonywanych czynności, czy można działać w pamięci?
7 kwi 14:27
Jakub: Napisałeś "najpierw sprawdziłem, czy funkcja jest rosnąca, czy malejąca (zerkając na a)".
Funkcja kwadratowa nie jest cała rosnąca lub cała malejąca. Gdy a>0 to wykres najpierw maleje,
a później rośnie. Gdy a<0 to to wykres najpierw rośnie, a później maleje. Reszta Twojego wpisu
jest dobra.
Oczywiście nie musisz tak bardzo rozpisywać jak u mnie. Ja tak dużo piszę, aby czytający
zrozumiał, co zrobiłem. Ty możesz zapisać to w skróconej formie, a sprawdzający i tak
zrozumie, co miałeś na myśli. Po prostu pisz, tak aby sprawdzający, wiedział, że Ty wiesz, o
co w tym chodzi

7 kwi 16:53
zbyszko: ajj, oczywiście chodziło mi o to, w którą stronę jest skierowana (czy w górę, czy w dół).
Musiałem się pomylić

11 kwi 18:14
Kamila: Wspaniała strona dla humanistów! Jak dla mnie zobrazowane wszystko w dość jasny sposób i
najważniejsze na konkretnych przykładach. Często korzystam przy powtórkach do matury.

3 lis 14:36
Yeti: bez sensu z liczeniem tego wierzcholka w tym przykladzie zdecydowanie wystarczy zaznaczyc 3
punkty −1,0,oraz 1 i narysowac pochylą czesc paraboli i od razu widac gdzie max a gdzie min,
1 sty 23:13
basia:
25 kwi 21:11
maestro: A co jesli nie jest podany przedział?
26 kwi 13:22
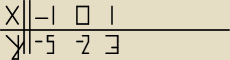 ten rysunek jest dla zobrazowania tego co chcę powiedzieć, gdybym nie wyrażał się jasno
ten rysunek jest dla zobrazowania tego co chcę powiedzieć, gdybym nie wyrażał się jasno  a moje pytanie jest następujące: czy można zrobić taką tabelkę zamiast się rozpisywać tak jak w
przedstawionym zadaniu?
a moje pytanie jest następujące: czy można zrobić taką tabelkę zamiast się rozpisywać tak jak w
przedstawionym zadaniu?
 Najważniejsze w tego typu zadaniach jest ustalić, czy wierzchołek leży w przedziale czy nie.
Jeżeli wierzchołek funkcji leży w przedziale <−1,1> to najmniejsza wartość jest właśnie w tym
wierzchołku, a największą wartość sobie wybierasz z tych dwóch z krańców przedziału, czyli dla
x=−1 i x=2.
Gdy wierzchołek nie leży wewnątrz przedziału to sytuacja jest prosta. Liczysz wartości na
krańcach przedziału i z nich wybierasz najmniejszą i największą wartość przedziału.
Tak więc najważniejsze jest policzenie xw na początku rozwiązywania i ustalenie czy należy do
<−1,1>.
Zobacz na te rysunki. Wiem, że są kiepskie, ale wyobraź sobie, że to są fragmenty parabol. Na
lewym i prawym rysunku masz identycznie położone trzy zielone punkty. Na lewym rysunku
narysowałem parabolę, która ma najmniejszą wartość w wierzchołku. Na prawym rysunku
narysowałem parabolę (fragment jej prawego ramienia), która ma najmniejszą wartość w skrajnym
lewym zielonym punkcie.
Jak widzisz trzy jednakowe punkty i dwa różne najmniejsze wartości.
Nie możesz ustalić najmniejszej wartości na podstawie tylko trzech punktów, ponieważ nie jesteś
w stanie określić tylko na podstawie tych trzech punktów, czy wierzchołek leży w <−1,1> czy
nie, dopóki nie policzysz xw.
Zauważ, że na lewym rysunku mimo, że punkty są rosnące, to funkcja nie jest rosnąca w całym
<−1,1>.
Najważniejsze w tego typu zadaniach jest ustalić, czy wierzchołek leży w przedziale czy nie.
Jeżeli wierzchołek funkcji leży w przedziale <−1,1> to najmniejsza wartość jest właśnie w tym
wierzchołku, a największą wartość sobie wybierasz z tych dwóch z krańców przedziału, czyli dla
x=−1 i x=2.
Gdy wierzchołek nie leży wewnątrz przedziału to sytuacja jest prosta. Liczysz wartości na
krańcach przedziału i z nich wybierasz najmniejszą i największą wartość przedziału.
Tak więc najważniejsze jest policzenie xw na początku rozwiązywania i ustalenie czy należy do
<−1,1>.
Zobacz na te rysunki. Wiem, że są kiepskie, ale wyobraź sobie, że to są fragmenty parabol. Na
lewym i prawym rysunku masz identycznie położone trzy zielone punkty. Na lewym rysunku
narysowałem parabolę, która ma najmniejszą wartość w wierzchołku. Na prawym rysunku
narysowałem parabolę (fragment jej prawego ramienia), która ma najmniejszą wartość w skrajnym
lewym zielonym punkcie.
Jak widzisz trzy jednakowe punkty i dwa różne najmniejsze wartości.
Nie możesz ustalić najmniejszej wartości na podstawie tylko trzech punktów, ponieważ nie jesteś
w stanie określić tylko na podstawie tych trzech punktów, czy wierzchołek leży w <−1,1> czy
nie, dopóki nie policzysz xw.
Zauważ, że na lewym rysunku mimo, że punkty są rosnące, to funkcja nie jest rosnąca w całym
<−1,1>.
 Dziękuję za pomoc
Dziękuję za pomoc 
 a zawsze obliczamy p i q
a zawsze obliczamy p i q


