kari: jesteście zajebiści


! xD 15 lat pamiętam ten conatgens... z egzaminów wstępnych do
ogólniaka. Właśnie zobaczyłam dziś ten wzór drugi raz w życiu − dzięki! Absolutnie nie
rozumiem z tego wzoru nic. Podobnie zresztą, jak nie rozumiałam wtedy, gdy wkuwałam go na
pamięc... ale pięknie wygląda i cieszę się, jestem wręcz z siebie duma, że przez bite 15 lat
pamiętałam go z przygotowań do egzaminu pisemnego z matmy do ogólniaka.
Dziś już mam od daaaawna wykształcenie wyższe (na UW, kierunek bardziej humanistyczny pewnie
niż sami prekursorzy humanizmu − dziennikarstwo), co nie znaczy, że ten wzór kiedykolwiek mi
się do czegokolwiek przydał....

Pozdrawiam serdecznie całą redakcję tego serwisu,
Karina,
szczęśliwa absolwentka XVII LO w Warszawie, im. Andrzeja Frycza−Modrzewskiego....

16 kwi 01:57
Jakub: Matematyka rzadko się przydaje w zwyczajnym życiu, jeżeli nie wykonuje się zawodu, gdzie trzeba
coś policzyć. Liczą się umiejętności, jakie się zdobyło przy nauce matematyki. Głównie chodzi
o umiejętność krytycznego, logicznego myślenia. Takie mi się nasuwa porównanie
militarystyczne. Żołnierze nie po to robią pompki, aby na wojnie je ćwiczyć. Liczy się
sprawność fizyczna jaką się przy tym zdobędzie.
16 kwi 17:18
Tuśka: Wie ktoś ile pięciokąt ma osi?
27 kwi 18:44
Tuśka: Foremny pięciokąt
27 kwi 18:50
Jakub:
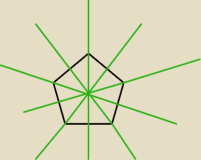
Chyba ci chodzi o osie symetrii pięciokąta foremnego (zobacz
899). Narysowałem pięciokąt
foremny i jego wszystkie osie symetrii.
27 kwi 20:01
Janusz88: witam czy ktoś mi poda wzór na wysokość i przekątną pięciokąta foremnego
24 wrz 18:50
Karolinka maturzystka: A czy te wszystkie zwory na pięciokąt są w tablicach maturalnych?
1 maj 14:26
Jakub: Na pięciokąt nie. Wzór na pole jednak prosto wyprowadzić. Kliknij niebieskie > > na poprzedniej
stronie przy wzorze.
1 maj 14:33
kali: czy ogarnia ktoś wzór na wysokość pięciokąta? ewentualnie przybliżoną liczbę przez którą trzeba
pomnożyć a, żeby wyszło h?
25 maj 00:44
Jakub:
Zapewne chodzi ci o pięciokąt foremny. Wysokość takiego pięciokąta to ten zielony odcinek na
rysunku. Jego długość to
h = x + r
Kąt α = 54
o Widać to też na stronie
879.
Długości x i r można wyliczyć z funkcji trygonometrycznych (zobacz
397)
r * cos54
o = a/2 /:cos54
o
| | a | | a | |
h = |
| tg54o + |
| |
| | 2 | | 2cos54o | |
26 maj 23:38
jabadababum: podawanie wzoru z ctg jest troche bez sensu chyba, bo przeciez ani w kalkulator tego nie
wbijemy ani nic, nie lepiej po prostu podać go z tg? Ja osobiście od razu przerobiłem go na
tg i moze wygląda
troche gorzej ale praktyczniejszy na pewno

5 gru 19:15
Jakub: Wystarczy pamiętać, że cotangens jest odwrotnością tangensa i można liczyć.
W tangensem wzór będzie wyglądał trochę gorzej, więc na razie zostaje z cotangensem

8 gru 02:30

 ! xD 15 lat pamiętam ten conatgens... z egzaminów wstępnych do
ogólniaka. Właśnie zobaczyłam dziś ten wzór drugi raz w życiu − dzięki! Absolutnie nie
rozumiem z tego wzoru nic. Podobnie zresztą, jak nie rozumiałam wtedy, gdy wkuwałam go na
pamięc... ale pięknie wygląda i cieszę się, jestem wręcz z siebie duma, że przez bite 15 lat
pamiętałam go z przygotowań do egzaminu pisemnego z matmy do ogólniaka.
Dziś już mam od daaaawna wykształcenie wyższe (na UW, kierunek bardziej humanistyczny pewnie
niż sami prekursorzy humanizmu − dziennikarstwo), co nie znaczy, że ten wzór kiedykolwiek mi
się do czegokolwiek przydał....
! xD 15 lat pamiętam ten conatgens... z egzaminów wstępnych do
ogólniaka. Właśnie zobaczyłam dziś ten wzór drugi raz w życiu − dzięki! Absolutnie nie
rozumiem z tego wzoru nic. Podobnie zresztą, jak nie rozumiałam wtedy, gdy wkuwałam go na
pamięc... ale pięknie wygląda i cieszę się, jestem wręcz z siebie duma, że przez bite 15 lat
pamiętałam go z przygotowań do egzaminu pisemnego z matmy do ogólniaka.
Dziś już mam od daaaawna wykształcenie wyższe (na UW, kierunek bardziej humanistyczny pewnie
niż sami prekursorzy humanizmu − dziennikarstwo), co nie znaczy, że ten wzór kiedykolwiek mi
się do czegokolwiek przydał....  Pozdrawiam serdecznie całą redakcję tego serwisu,
Karina,
szczęśliwa absolwentka XVII LO w Warszawie, im. Andrzeja Frycza−Modrzewskiego....
Pozdrawiam serdecznie całą redakcję tego serwisu,
Karina,
szczęśliwa absolwentka XVII LO w Warszawie, im. Andrzeja Frycza−Modrzewskiego.... 
 Chyba ci chodzi o osie symetrii pięciokąta foremnego (zobacz 899). Narysowałem pięciokąt
foremny i jego wszystkie osie symetrii.
Chyba ci chodzi o osie symetrii pięciokąta foremnego (zobacz 899). Narysowałem pięciokąt
foremny i jego wszystkie osie symetrii.
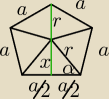
 Zapewne chodzi ci o pięciokąt foremny. Wysokość takiego pięciokąta to ten zielony odcinek na
rysunku. Jego długość to
h = x + r
Kąt α = 54o Widać to też na stronie 879.
Długości x i r można wyliczyć z funkcji trygonometrycznych (zobacz 397)
Zapewne chodzi ci o pięciokąt foremny. Wysokość takiego pięciokąta to ten zielony odcinek na
rysunku. Jego długość to
h = x + r
Kąt α = 54o Widać to też na stronie 879.
Długości x i r można wyliczyć z funkcji trygonometrycznych (zobacz 397)

