math: Skąd wiadomo, że odcinki podzielone przez promienie są równe, tj. y=y, z=z, etc.? Z czego to wynika?

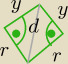
Jakub: Narysowałem fragment rysunku z poprzedniej strony. Zauważ, że każdy z tych dwóch trójkątów: 1) ma bok o długości r (promień okręgu) 2) ma wspólny bok d (koloru szarego) 3) ma kąt prosty (promień poprowadzony do punktu styczności, jest zawsze prostopadły do stycznej) Na podstawie twierdzenia Pitagorasa można napisać dla każdego trójkąta: y = √d²−r² Jak widzisz, odcinki, które oznaczyłem jako y, są sobie równe. W ten sam sposób można udowodnić równość odcinków x, w, z.

math: Teraz widzę zależność, bardzo dziękuję Ta strona to kawał dobrej roboty, gratuluję.

Bazyl: Okrąg można wpisać w czworokąt wtedy i tylko wtedy gdy sumy miar jego przeciwległych boków są równe. Bardzo proszę o dowód tego twierdzenia w drugą stronę, bo na stronie jest tylko w jedną, a muszę znać twierdzenie dowodzone w obie strony.