 Tak do szkoły nie chodzę już od dawna, ale muszę sobie przypomnieć pewne zagadnienia. Ale do
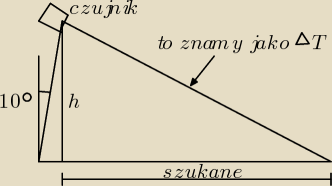
rzeczy, mam czujnik odległości który jest zamocowany na stałej wysokości h=4cm, i jest
odchylony od
pionu pod kątem 10 stopni. Czujnik dostarcza mi danych o odległości do przeszkody/podłoża.
Teraz muszą przypomnieć sobie jak zrobić wzór, aby policzyć z tych danych długość podstawy
takiego
trójkąta, czyli odległość rzeczywistą od czujnika do celu.
Znaczy ogólnie potrzebuję tylko wzorów na obliczenie odległości, resztą i tak bezie zajmował
się mikroprocesor.
Tak do szkoły nie chodzę już od dawna, ale muszę sobie przypomnieć pewne zagadnienia. Ale do
rzeczy, mam czujnik odległości który jest zamocowany na stałej wysokości h=4cm, i jest
odchylony od
pionu pod kątem 10 stopni. Czujnik dostarcza mi danych o odległości do przeszkody/podłoża.
Teraz muszą przypomnieć sobie jak zrobić wzór, aby policzyć z tych danych długość podstawy
takiego
trójkąta, czyli odległość rzeczywistą od czujnika do celu.
Znaczy ogólnie potrzebuję tylko wzorów na obliczenie odległości, resztą i tak bezie zajmował
się mikroprocesor.
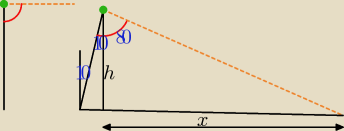 Trochę niejasno opisane. Rozumiem to tak. Czujnik (zielona kropka) jest zamocowany na jakimś
pręcie. Promienie, które wysyła w celu zlokalizowania obiektu (pomarańczowy kolor) są pod
kątem prostym (90o − czerwony kolor) do pręta. Dobrze to widać na rysunku po lewej.
Na rysunku po prawej pręt został odchylony od piony o 10o i promienie padają na ziemie w
odległości x od boku h. Kąt 10o jest w dwóch miejscach, co zaznaczyłem na rysunku (niebieskie
kolor).
Kąt między bokiem h i promieniami jest równy 80o (90o−10o). Odległość x można policzyć z
tangensa (zobacz 397).
Trochę niejasno opisane. Rozumiem to tak. Czujnik (zielona kropka) jest zamocowany na jakimś
pręcie. Promienie, które wysyła w celu zlokalizowania obiektu (pomarańczowy kolor) są pod
kątem prostym (90o − czerwony kolor) do pręta. Dobrze to widać na rysunku po lewej.
Na rysunku po prawej pręt został odchylony od piony o 10o i promienie padają na ziemie w
odległości x od boku h. Kąt 10o jest w dwóch miejscach, co zaznaczyłem na rysunku (niebieskie
kolor).
Kąt między bokiem h i promieniami jest równy 80o (90o−10o). Odległość x można policzyć z
tangensa (zobacz 397).
| x | ||
tg80o = | ||
| h |
| x | ||
5,67 = | /*h | |
| h |
| h | h | |||
cos80o = | ctg80o = | |||
| p | x |
 Wstawiłeś za p wartość z x i dlatego wysokość h odbiegła od początkowych 4cm.
Wstawiłeś za p wartość z x i dlatego wysokość h odbiegła od początkowych 4cm.