Paweł: dla przykładu po co w ogóle robi się takie założene mógłbyś podać długości boków z których
nieda sie zbudować trójkąta
19 kwi 23:45
Jakub:
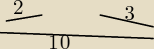
Przykładowo z odcinków 2,3,10 nie zbudujesz trójkąta, ponieważ 2+3<10.
20 kwi 16:52
prb: Dobrze, a czy ktos moze wyjasnic w jaki sposób po dlugosciach odcinków możemy określic czy
trojkat jest trojkatem rozwartokatnym lub ostrokatnym, ? Dla prostokatnego a2+b2 = c2 tak ?
28 kwi 15:00
Jakub: Jeżeli kwadrat długości dowolnego boku jest mniejszy od sumy kwadratów długości pozostałych
boków, to trójkąt jest ostrokątny.
Przykładowo dla boków 7,10,12 mam
72 < 102 + 122 (prawda, bo 49 < 100 + 144)
102 < 72 + 122 (prawda, bo 100 < 49 + 144)
122 < 102 + 72 (prawda, bo 144 < 100 + 49)
Trójkąt o bokach 7,10,12 jest ostrokątny.
Gdyby wyszło, że lewa strona jest większa do prawej w którymś wierszu, to trójkąt byłby
rozwartokątny.
Gdyby wyszło, że lewa strona jest równa prawej w którymś wierszu, to trójkąt byłby
prostokątny.
28 kwi 20:24
fik: Wydaje mi się, że Twoje twierdzenie Jakub jest bezpośrednio związane z twierdzeniem cosinusów.
A to już rozszerzenie, więc proponuję dodać takie zadanie na rozszerzenie aby ludzie wiedzieli
jak sprawdzać czy kąt jest ostry.

4 maj 19:28
Jakub: Racja

Odpowiadając prb korzystałem z twierdzenia cosinusów. Myślę, że ci co mają
rozszerzenie, powinni się posługiwać wprost twierdzeniem cosinusów do ustalania czy kąt jest
ostry, a nie tym co napisałem wyżej. To jest dla ludzi z podstawy i nie chciałem im mieszać z
twierdzeniem cosinusów, więc je zastosowałem, choć nie wymieniłem z nazwy.
4 maj 19:48
Joker: a czy to nie powinien być rozważany najdłuższy bok w stosunku do dwóch pozostałych? bo ciągle
mi się to tłucze tak po głowie
11 gru 22:26
Jakub: Dla wszystkich boków trójkąta powinna te nierówności być prawdziwe. Nie tylko
najdłuższy < suma dwóch pozostałych.
12 gru 00:35
Szymon: Czemu w podreczniku szkolnym mam napisne że jeśli dwa boki trójkąta maja długości 4cm i 10cm to
trzecim bokiem nie moze byc równy 13,(9) . Przecież 13,(9) < 10+4 . Z góry dziekuje za odp.
25 lut 11:18
Jakub: Szkoda, że podręczniki nie mają linka "komentarz do tej strony".
Wtedy ci by autor odpowiedział

. Tak to ja muszę

13,(9) = 14, a nie jak napisałeś 13,9 < 14. Wiem, że to trudno pojąć, ale 13,(9) = 14.
Dowód jest taki.
13,(9) = 13,99999.... i tych 9−tek jest nieskończenie wiele. Pisząc każdą kolejną dziewiątkę
zbliżam się do 14. W ten sposób mogę się zbliżyć dowolnie blisko do 14. Ponieważ tych 9−tek
jest nieskończenie wiele, to liczba 13,(9) jest nieskończenie blisko 14, czyli jest równa 14.
Trudno to sobie wyobrazić, ale tak jest. Jak to ciebie dalej nie przekonuje, to spróbuj
zamienić 13,(9) na ułamek zwykły tak jak na
1129. Zobaczysz, co ci wyjdzie.
Jeżeli 13,(9) = 10 + 4, to oczywiście 13,(9); 10 i 4 nie mogą być bokami trójkąta, ponieważ
dowolny bok musi być MNIEJSZY od sumy pozostałych.
25 lut 20:33
Semir: Co do twojego drugiego postu i tej teorii jeśli mamy boki 2, 3, 10 to 3 jest mniejsze od 10+2.
Mam dowolny bok czyli 3 i jest on mniejszy od sumy pozostałych i weź mi teraz to wytłumacz.
28 mar 15:52
Przemo: To twierdzenie jest niepoprawne. Jeżeli weźmiemy pod uwagę trójkąt prostokątny a2+b2=c2
Z tego wynika, że
c≤a+b
6 lis 23:30
Jakub: Jest poprawne. Weź np. liczby 3, 4, 5. To są długości boków prostokąta, bo 32 + 42 = 52.
Nierówność trójkąta też jest spełniona 5 ≤ 3+4.
7 lis 00:35
NK: Ja mam tylko drobną uwagę, może się czepiam, ale wbija mi się do głowy przez całe 3 lata
studiów żemówi się długość boku a nie bok

Może to się przydać uczniom którzy wchodzą na tą stronkę bo nauczyciel zazwyczaj zwraca uwagę
na wymowę.
9 gru 11:02
A,: Super strona. Dla mnie matematyka to czarna magia, tutaj jest wszystko fajnie wytłumaczone.
Pozdrawiam.

18 gru 19:15
yahoo: podziwiam cię jakub, że nie załamujesz się psychicznie nad niektórymi komentarzami, bo mnie
czasami korci by zatłuc moją wieczorną lampką niektórych użytkowników tej strony.
pozdrawiam
3 sty 04:53
Jakub: Nie jest źle. Większość komentarzy jest na wysokim poziomie. Pewnie to dzięki temu, że to
strona o matematyce.
3 sty 10:25
twoja mama: Fajne
22 sty 17:49
Bartek : Nigdy tego nie pisałem, ale uważam, że tu przychodzą na prawdę inteligentni ludzie. Nie ma tu
żadnych zabezpieczeń antyspamowych (żadnej rejestracji) a jeszcze nie widziałem tu ani jednej
awantury. Niestety nie mam tego samego zdania o forach dotyczących programowania. Tam są
jakieś co chwila...
29 cze 15:21
mallynowa: mam takie pytanie bo wiem że jest jeszcze jedna reguła tylko z wartoscią bezwzględną mógłby
ktoś podać je ?
22 sie 15:48
KIKA: Wystarczy sprawdzić, czy najdłuższy bok trójkąta jest mniejszy od pozostałych i wtedy nie
sprawdzamy pozostałych boków, a więc gdy np boki są 2,3,6 to sprawdzam czy najdłuższy bok,
czyli 6 jest mniejszy od sumy 3 i 4. 6<3+4 a więc trójkąt da się zbudować.
6 lis 21:59
[N[458]]: |a−b|<c <a+b
Widziałem też taką postać nierówności trójkąta. Dla przykładu komentarz Pana Jakuba z 20.
kwietnia o 16.52. 3<10+2 to prawda, lecz 10−2 nie jest mniejsze od 3, więc trójkąt nie
powstanie
8 wrz 19:13
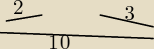 Przykładowo z odcinków 2,3,10 nie zbudujesz trójkąta, ponieważ 2+3<10.
Przykładowo z odcinków 2,3,10 nie zbudujesz trójkąta, ponieważ 2+3<10.

 Odpowiadając prb korzystałem z twierdzenia cosinusów. Myślę, że ci co mają
rozszerzenie, powinni się posługiwać wprost twierdzeniem cosinusów do ustalania czy kąt jest
ostry, a nie tym co napisałem wyżej. To jest dla ludzi z podstawy i nie chciałem im mieszać z
twierdzeniem cosinusów, więc je zastosowałem, choć nie wymieniłem z nazwy.
Odpowiadając prb korzystałem z twierdzenia cosinusów. Myślę, że ci co mają
rozszerzenie, powinni się posługiwać wprost twierdzeniem cosinusów do ustalania czy kąt jest
ostry, a nie tym co napisałem wyżej. To jest dla ludzi z podstawy i nie chciałem im mieszać z
twierdzeniem cosinusów, więc je zastosowałem, choć nie wymieniłem z nazwy.
 . Tak to ja muszę
. Tak to ja muszę  13,(9) = 14, a nie jak napisałeś 13,9 < 14. Wiem, że to trudno pojąć, ale 13,(9) = 14.
Dowód jest taki.
13,(9) = 13,99999.... i tych 9−tek jest nieskończenie wiele. Pisząc każdą kolejną dziewiątkę
zbliżam się do 14. W ten sposób mogę się zbliżyć dowolnie blisko do 14. Ponieważ tych 9−tek
jest nieskończenie wiele, to liczba 13,(9) jest nieskończenie blisko 14, czyli jest równa 14.
Trudno to sobie wyobrazić, ale tak jest. Jak to ciebie dalej nie przekonuje, to spróbuj
zamienić 13,(9) na ułamek zwykły tak jak na 1129. Zobaczysz, co ci wyjdzie.
Jeżeli 13,(9) = 10 + 4, to oczywiście 13,(9); 10 i 4 nie mogą być bokami trójkąta, ponieważ
dowolny bok musi być MNIEJSZY od sumy pozostałych.
13,(9) = 14, a nie jak napisałeś 13,9 < 14. Wiem, że to trudno pojąć, ale 13,(9) = 14.
Dowód jest taki.
13,(9) = 13,99999.... i tych 9−tek jest nieskończenie wiele. Pisząc każdą kolejną dziewiątkę
zbliżam się do 14. W ten sposób mogę się zbliżyć dowolnie blisko do 14. Ponieważ tych 9−tek
jest nieskończenie wiele, to liczba 13,(9) jest nieskończenie blisko 14, czyli jest równa 14.
Trudno to sobie wyobrazić, ale tak jest. Jak to ciebie dalej nie przekonuje, to spróbuj
zamienić 13,(9) na ułamek zwykły tak jak na 1129. Zobaczysz, co ci wyjdzie.
Jeżeli 13,(9) = 10 + 4, to oczywiście 13,(9); 10 i 4 nie mogą być bokami trójkąta, ponieważ
dowolny bok musi być MNIEJSZY od sumy pozostałych.
 Może to się przydać uczniom którzy wchodzą na tą stronkę bo nauczyciel zazwyczaj zwraca uwagę
na wymowę.
Może to się przydać uczniom którzy wchodzą na tą stronkę bo nauczyciel zazwyczaj zwraca uwagę
na wymowę.
