filip: ostatni przykład : chyba łatwiej przemnożyc obie strony rownania przez ctgx +ctgy i juz koniec a nie konsekwentnie trzymac sie zasady wymnazanie lewej az wyjdzie prawa strona

Jakub: Lepiej nie. Mnożysz równanie, które masz udowodnić, czy jest prawdziwe czy fałszywe. Jak je pomnożysz przez ctgx + ctgy to je zmienisz i będziesz miał już inne równanie. Wprawdzie można napisać, że jest ono równoważne poprzedniemu. Większość osób tego jednak nie robi i przekształca równanie, aż wyjdzie prawda np. sinx = sinx. Kolejność powinna być w zasadzie odwrotna. Powinno się wyjść z równania prawdziwego i dojść do równania, które mamy udowodnić. Problem w tym, że to jest dużo trudniejsze. Z tego powodu lepiej jest robić jak ja, czyli wyjść z lewej strony, przekształcać, przekształcać, przekształcać i dojść do prawej. Można też odwrotnie.

patryk: pierwszy przykład: Czy w tym przykładzie na pewno lewa strona równa się prawe? bo próbowałem to jakoś rozwiaząć i mi nie wychodzi

Jakub: Na pewno. Niżej masz rozwiązanie.

Travis: Nie rozumiem skąd w pierwszym przykładzie, pod koniec, z ...= cos²x − sin²x = 1 − sin² − sin²x =.... Dokładniej rzecz biorąc, skąd wzięła się ta jedynka?

Jakub: Z jedynki trygonometrycznej Travis. Zobacz stronę 450. Tam masz sin²α + cos²α = 1 po przeniesieniu sin²α na prawo cos²α = 1 − sin²α

big al: 1.Czemu w pierwszym przykładzie

	sin2x		cos2x		sin2x
1 −		=		−		? Chodzi mi o tę
	cos2x		cos2		cos2x

	cos2x		x
jedynkę. Przecież		=		, a nie jeden...
	cos2		1

	cos2x		sin2x
2. Czemu możemy wykonać odejmowanie		−		, skoro mianowniki
	cos2		cos2x

się nie zgadzają? Z góry dziękuję za rozwianie wątpliwości

Jakub: To pomyłka. Zjadło mi x przy cos². Dzięki, już poprawiłem. Nie istnieje w matematyce sam cos czy cos². Funkcja cos jest zawsze z czegoś. Podobnie jak nie istnieje samo podnoszenie do kwadratu ². Potęgować zawsze musimy coś. Dlatego błędnie

	cos2x		x
napisałeś, że		=		. To równanie nie ma sensu matematycznego. Nie można
	cos2		1

traktować cos²x jak mnożenia. Oczywiście twój błąd wynika z mojego

big al: Dzięki za rzucenie nowego światła na mroczny świat funkcji trygonometrycznych

big al: A dlaczego w drugim przykładzie (cos²x − sin²x)(cos²x + sin²x) = cos²x − sin²x? Zgodnie ze wzorem skróconego mnożenia (a−b)(a+b) = a² − b², ale tutaj współczynniki już są podniesione do kwadratu − więc po wymnożeniu wracamy do punkty wyjścia i otrzymujemy cos⁴x − sin⁴x...

mm: Własnie skad w drugim przykladzie sie to wszystko bierze bo nic z tego nie rozumiem.

Jakub: Drugi nawias jest równy jeden. Jedynka trygonometryczna: sin²α+cos²α = 1 (zobacz 450)

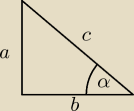
dbdf: Zastanawiam się czy można by rozwiązać np: to ostatnie zadanie, podstawiając zamiast tgx a/b oraz zamiast ctgx b/a

a   a   +   b   b		2a     b
	=		=
b   b   +   a   a		2b     a

2a

a

2a2

a*a

a

a

*

=

=

=

*

=tgx*tgx

b

2b

2b2

b*b

b

b

L=P

dbdf: Czy na maturze miałbym maksa punktów za to

Jakub: Potraktowałeś x (kąt) z równania na poprzedniej stronie, jakby to był kąt ostry. Nie ma jednak o tym mowy w treści zadania. Litera x oznacza wszystkie kąty, także te większe od 90^o. Ty udowadniasz to dla kąta ostrego. Twoje definicje "działają", jeżeli α jest kątem ostrym. Tak wiec, jakieś punkty byś dostał, ale na pewno nie maksa.

dbdf: ok, dzięki, rozumiem, to dla pewności lepiej będę robić to Twoim sposobem

Joop: Dla chetnych inny sposob rozwiazania drugiego rownania: cos⁴x − sin⁴x = cos²x * cos²x − sin²x * sin²x = (1 − sin²x) * cos²x − (1 − sin²x) * sin²x = cos²x − sin²x * cos²x − sin²x + sin²x * cos²x = cos²x − sin²x = P

Majka: Wszystko fajnie, tylko szkoda, że nie ma zamieszczonej dziedziny funkcji w rozwiązaniu Moja nauczycielka ciągle powtarza, że jest ona najważniejsza i od niej należy zaczynać zadanie...

snoop: A skąd to wyszło cos²x−sin²x= 1−sin²x−sin²x ?

Jakub: Skorzystałem z jedynki trygonometrycznej (zobacz 450) sin²x + cos²x = 1 cos²x = 1−sin²x i za cos²x podstawiam 1−sin²x.

snoop: Aha, czyli można sobie tak to przerzucać na rożne strony OK. Dziękuje.

Stokrotek:

kkkasiula: u mnie też z tą dziedziną jest masakra całe życie nam każe wyznaczać te dziedziny i często jest z tym problem szkoda że tu nie jest omówione kiedy się te założenia robi i jak bo kiedyś przy dokładnym omawianiu tego działu to wiedziałam, a teraz nie pamiętam

Jakub: W zadaniach na udowodnienie tożsamości trygonometrycznej zazwyczaj nie ma w rozwiązaniach dziedziny. Może to nie do końca poprawne, ale w takich zadaniach nie dziedzina jest najważniejsza.

Astaroth: Tylko jedno pytanie − w ostatnim zadaniu nie lepiej byłoby napisać " tgy=ctgx " i liczyć na tej podstawie?

Jakub: Skąd wiadomo, że tgy = ctgx. Nie ma tego w tekście zadania, ani z niczego nie wynika. Nie mogę sobie tak po prostu dopisać, aby mi się łatwiej liczyło.

Mati: Nie rozumiem skąd to wzięło się w 3 przykładzie: (chodzi o to co w nawiasie) ^sinx_cosx = (^sin2x_sinxcosx + ^cos2x_sinxcosx)

wasp: Mam pytanie co do sprowadzania ulamkow do wspólnego mianownika w trzecim przykładzie. Dlaczego z ^sin_cos + ^cos_sin wyszło ^sin2+cos2_cos*sin?

niekumaty: dlaczego w pierwszym przyklładnie jest w 1 podstawione cos2x/cos2x a nie np sinus?

TheJoker: Wiedząc że 10 oblicz x oraz wyznacz zależność A od prędkości spodka w próżni

Jakub: Szkoda, że sobie nawet nie zdajesz sprawy, jak poważne przez przypadek udało ci się zadać. Długość boku A w zależności od prędkości. http://fizyka.pisz.pl/strona/87.html

Gustlik: Jakubie, proponuję sposób udowadniania tożsamości metodą równań równoważnych, czyli zamiast iść od lewej do prawej lub odwrotnie, stopniowo przekształcać i upraszczać obie strony jak przy rozwiązywaniu równań. Możemy oprócz wzorów trygonometrycznych stosować takie same zasady przekształcania równań jak przy rozwiązywaniu równań, np. przenosić wyrażenia na drugą stronę zmieniając znak, mnożyć i dzielić obustronnie przez liczby lub wyrażenia algebraiczne itp. doprowadzając jednocześnie obie strony równości do coraz prostszej postaci. Możemy w ten sposób łatwo pozbywać się trudnych do przekształcania wyrażeń algebraicznych, np. ułamków, zwłaszcza piętrowych, co znacznie upraszcza obliczenia. Rozwiązując szkolną metodą lewa→prawa mamy działanie, a nie równanie i nie można wówczas pozbyć się takich niewygodnych wyrażeń. Dowodem poprawności tożsamości powinien być wynik, w którym po lewej i prawej stronie otrzymamy to samo wyrażenie, np. 0=0, 1=1, sinα=sinα, 1−cosα=1−cosα itp.

Gustlik: Przykład tożsamości sprawdzonej metodą "równaniową":

	1−tg2x
1−2sin2x=		/*(1+tg2x)
	1+tg2x

(1−2sin²x)(1+tg²x)=1−tg²x

	sin2x		sin2x
(1−2sin2x)(1+		)=1−
	cos2x		cos2x

	cos2x+sin2x		cos2x−sin2x
(1−2sin2x)(		)=		/*cos2x
	cos2x		cos2x

(1−2sin²x)(cos²x+sin²x)=cos²x−sin²x Ponieważ cos²x+sin²x=1, mamy 1−2sin²x=cos²x−sin²x Podstawiając cos²x=1−sin²x po prawej stronie mamy 1−2sin²x=1−2sin²x L=P, c.n.d. I nie mamy ułamków piętrowych, a zwykłe ułamki można było wyeliminować obustronnym mnożeniem przez wspólny mianownik.

Jakub: Racja, że metoda działań równoważnych jest w wielu przypadkach prostsza. Jednak mój sposób wydaje mi się bardziej ,,elegancki''. Przekształcam jedną stronę, otrzymuję drugą, więc równość obu stron jest oczywista. W Twoim sposobie otrzymuje się np. 1 = 1 lub 1−2sin²x = 1−2sin²x i trzeba napisać jakiś komentarz, co to właściwie oznacza.

Gustlik: Warto znać metodę równań równoważnych, dodam, że dużo uczniów woli ten sposób od "szkolnego", bo na ogół jest łatwiejszy.

Gustlik: Jakubie, metoda równań równoważnych jest prostsza też z innego powodu: licząc "standardową" metodą licząc od od lewej do prawej można czasami pójść złą drogą i "zabrnąć w ślepą uliczkę", z której potem ciężko wyjść, albo nie zauważyć, jak można uprościć dane wyrażenie, a rozwiązując metodą równań upraszczamy obie strony i minimalizujemy ryzyko błędu, bo widzimy zależność. Ja w tej chwili patrzę na problem z punktu widzenia ucznia, który zobaczy jakieś megaskomplikowane wyrażenie typu ułamek piętrowy i zgłupieje, nawet jeżeli do tej pory ma dobrze. I nie zrobi zadania, bo nie będzie umiał z tego wybrnąć. Dlatego zdecydowanie NIE ZALECAM SZKOLNEJ METODY. Może jest bardziej elegancka, ale trudniejsza, nie dość, że łatwiej się pomylić, to jeszcze można zabrnąć i nie umieć z tego wyjść.

Gustlik: A komentarz jest prosty: Jeżeli otrzymałem wyrażenie typu 1−2sin²x=1−2sin²x to piszę L=P albo proste zdanie: "otrzymałem wyrażenie, w którym lewa strona jest równa prawej, a więc równość jest prawdziwa dla każdego x". Napisanie takiego komentarza jest o wiele prostsze, niż rozwiązywanie "szkolną" metodą i zajmuje kilka sekund, podczas gdy prostowanie megaskomplikowanych wyrażeń zajmuje o wiele wiecej czasu, nie wspominając, że mozna sie przy tym pogubić albo pomylić. Im mniej skomplikowanych wyrażeń, tym lepiej dla ucznia, zwłaszcza uczącego się matematyki na poziomie podstawowym. Poza tym nauczyciel lub egzaminator sprawdzający zadania będzie widział, jak uczeń dochodził do wyniku i uzna zadanie, jeżeli nie będzie błędów.

Gustlik: Jest jeszcze jedna sprawa, dla której ta metoda jest lepsza: spotkałem się wielokrotnie z zadaniami typu "sprawdź, czy podana równość jest tożsamością trygonometryczną". Jest podanych kilka równań, niektóre z nich są tożsamościami, niektóre nie są. I uczeń nie wie, które jest, a które nie jest. Będzie rozwiązywał szkolnym sposobem, pomyli się i wyjdzie mu, że dane równanie nie jest tożsamością, podczas gdy faktycznie jest albo na odwrót. I uczeń wtedy myśli, że widocznie to równanie nie jest tożsamością, bo w poleceniu napisali "sprawdź, czy jest to tożsamość". I ma źle. W zadaniach typu "sprawdź tożsamość" wiadomo, że jest to tożsamość, tylko musimy to wykazać. Jeżeli nie wyszło, wiadomo, że mamy błąd. A w zadaniach typu "sprawdź, czy jest to tożsamość" nie wiadomo, czy jest czy nie jest i jak nie wychodzi, to nie wiemy, czy mamy błąd, czy po prostu tak ma być. Rozwiązując równaniami nam to wyjdzie, a prawdopodobieństwo pomyłki jest dużo mniejsze i na uproszczonych wyrażeniach algebraicznych z obu stron łatwiej to sprawdzić.

titem: Gustlik: fajnie, ale trochę tl ; dr