kamil: czemu wzór na ctgα nie wyglada ctgα=cosα/sinα tam jest ze ctgα=1/tgα nie wiem wg czego w koncu mam robic

kamil: sorry chyba juz wiem doszedłem do tego ALe jakby Pan mógł to moze pan wytłumaczyc o co w tym wszystkim chodzi

Jakub: Może to ci pomoże:

	1
ctg α =
	tgα

	sinα
tgα =
	cosα

	1		1		cosα
ctg α =		=		=
	tgα		sinαcosα		sinα

m: Wszystko fajnie i zrozumiale opisane, tylko nie moge pojac dlaczego cosα ≤ 0

Jakub: Kliknij na poprzedniej stronie niebieski cosα<0, zobaczysz tabelkę. Tam będzie, że dla α∊(^π₂,π) funkcja ma wartości ujemne. Możesz to samo zobaczyć na wykresie cosinusa na stronie 427.

Magda: Skoro sinα=1/3 to cosα= x/3 czyli mając sin² + cos^α= 1 mogę zapisać to jako 1/9 + x²/9=1 ? Tylko że wtedy mi wychodzi mi inny wynik niż Tobie.. Czyli co robie źle?

Jakub: Dlaczego inny? ¹₉ + ^x2₉ = 1 ^x2₉ = 1 − ¹₉ ^x2₉ = ⁸₉ /*9 x² = 8 x = √8 = 2√2 lub x=−2√2

	x		2√2		2√2
cosα =		=		lub cosα = −
	3		3		3

Nie wiem, dlaczego za cosα wstawiasz ^x₃ zamiast samo x. Nie jest to błąd. Komplikujesz jednak rozwiązanie.

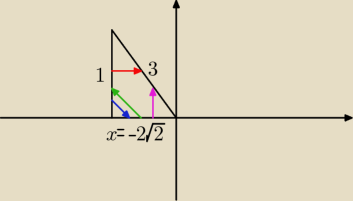
Gustlik: Można geometrycznie:

	1
sinα=		, kąt ćw. II
	3

x obliczam Pitagorasem: 3²=1²+x² 9=1+x² x²=8 x=2√2 v x=−2√2 − wybieram ujemną wartość x, bo w II ćw. odcięte x są ujemne

	−2√2		2√2
cosα=		=−
	3		3

	1		√2		√2
tgα=		=−		=−
	−2√2		2*2		4

	−2√2
ctgα=		=−2√2
	1

Astaroth: Nie wiem, czy pan Gustlik odwiedzi jeszcze tą stronę, ale dzięki dla niego, bo już myślałem, że robię źle, jak zobaczyłem sposób pana Jakuba

Mmm: Popieram, intuicyjnie też zrobiłam sposobem Gustlika i zanim zobaczyłam jego komentarz to przez moment też się obawiałam że źle kombinuję