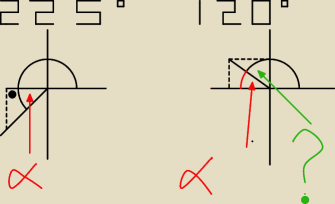
makaron: Witam, nie rozumiem dlaczego w przykładach dla 225 i 330 liczony przez Ciebie kąt zawiera się w rysowanym kącie, a dla przykładów 135 i 225 dorysowałeś (dopełniłeś osobnym kątem po drugiej stronie przeciwprostokątnej) osobny kąt. Aby lepiej pokazac o co mi chodzi, dodam rys. dla przykładowo różnie policzonych 225 i 120. Na obrazku po lewej liczony kąt zawiera się w kącie 225, a na obrazku po prawej liczony kąt nie zawiera się w 120. Czemu jest dorysowany, a nie znajduje się tam gdzie zielona strzałka?

Jakub: Prawdziwy powód jest taki, że tam gdzie jest zielona strzałka napisane jest 120^o i nie bardzo można wcisnąć 30^o. Jak widzisz jest to powód estetyczny a nie matematyczny . Jak chcesz to możesz liczyć z tego kąta 30^o między drugim ramieniem kąta a osią y. Ja policzyłem współrzędne punktu P z kąta 60^o. Nie ma to większego znaczenia, wyniki muszą wyjść i tak takie same.

Minis: Witam, jak to wybieramy dowolny punkt ? Zrobiłem to samo dla np −2 i 2 i wyszło inaczej niż dla −3 i 3, skąd mam wiedzieć dla jakich punktów liczyć ?

Minis: Jestem ułomny, robiłem to na jednym rysunku i pogmatwałem, wszystko jest dobrze, przepraszam za wprowadzenie w błąd

Dziadek: Dlaczego punkt który Pan wybrał to P=(−3,3) ? A nie P=(−5,5) który też tworzy kąt z osią OX ∡= 135°? Gdzie wynik sinusa, cos,tg,ctg dla P=(−5,5) jest całkiem inny. Dlaczego dla innych przykładów 120°, 330° wybrał Pan takie, a nie inne punkty?

Jakub: To jest obojętne, czy wybiorę punkt (−3,3), (−5,5) czy (−1,1). Dla tych wszystkich punktów druga półprosta tworzy z pierwszą półprostą kąt 135^o. To widać na rysunku. Wybrałem (−3,3) bo musiałem coś wybrać. Padło akurat na te współrzędne. Sinus, cosinus, tangens, cotangens dla współrzędnych (−5,5) wychodzi taki sam, jak dla współrzędnych (−3,3). Gdzieś robisz błąd w obliczeniach. Jak mi je napiszesz, to chętnie go znajdę. Dla kątów 120^o, 330^o wybierałem współrzędną x czy y też przypadkowo, ale drugą już liczyłem. Tak aby druga półprosta tworzyła z pierwszą półprostą odpowiedni kąt. Tutaj więcej przykładów 1721. Jak któryś jest niezrozumiały, to napisz pod nim komentarz, co jest niezrozumiałe.

Dziadek: faktycznie mój błąd w obliczeniach, dla każdego punktu te same wyniki, dziękuje!. dlaczego w tym zadaniu (dla 135°) podaje pan sinus (dla∡45°) = ³_3√2 a nie sin(dla∡135°) = ⁻³_3√2? i analogicznie w kolejnych przykładach 120°,225°, 330° dlaczego też podał pan sin,cos,tg,ctg dla tego danego trójkąta który nie zawiera się w danym kącie?

Jakub: Hmm. Na komentowanej stronie jest

	3
sin135o =		= ...
	3√2

czyli podaję jednak sinus dla 135^o a nie dla 45^o. Skąd biorę ten ułamek? Zobacz na definicję dowolnego kąta na stronie 417. Korzystanie z tej definicji polega na narysowaniu kąta w układzie współrzędnych, znalezieniu dowolnego punktu na drugim ramieniu i policzeniu z jego współrzędnych sinusa kąta. To właśnie zrobiłem. Znalazłem punkt P = (−3,3) i skorzystałem ze wzoru

	y
sinα =
	r

y = 3, a ,,r'' musiałem policzyć ze wzoru r = √x²+y². Analogicznie liczę cosinus, tangens, cotangens. To 45^o, zaznaczone w układzie współrzędnych, jest tam tylko po to, aby patrzący miał pewność, że kąt po drugiej stronie to 135^o = 180^o−45^o. Po prostu łatwiej poznać kąt 45^o niż 135^o. To jest jedyna funkcja 45^o w tym zadaniu.

Sejton: Do ustalenia położenia drugiego ramienia jest potrzebna ekierka tak, czy są inne sposoby?

Jakub: Po prostu rysujesz drugie ramię przez punkty przecięcia linii tworzących kratki na stronie.

dd: z treścią zadania jest chyba coś nie tak, dziwnie brzmi

kare: tg 135 stopni oblicz

Jakub: tg135^o = tg(180^o − 45^o) = tg(−45^o) = −tg45^o = −1