malinka: super materiał...bardzo przydatny
8 paź 12:01
Gustlik: Jakubie − pragnę tutaj zaproponować taki schematyczny rysunek, który ułatwia obliczanie funkcji
trygonometrycznych w trójkącie prostokatnym. Czy mógłbyś to dodatkowo zrobić na tej stronce?
Np. dla kąta α:
Rysuję trójkąt prostokątny, boki oznaczam literami a, b, c tak samo jak Ty,
Rysuję strzałki pomiędzy bokami i opisuje je oznaczeniami funkcji trygonometrzycznych kąda α,
strzałki pokazuja kierunek liczenia tych funkcji, a więc który bok przez który mam dzielić:
− dla sinα strzałka od przyprostokątnej a do przeciwprostokątnej c, narysowana przy drugim
kącie ostrym − przy kącie β,
− dla cosα strzałka od przyprostokątnej b do przeciwprostokątnej c, narysowana przy kącie α,
− dla tgα strzałka od przyprostokątnej a do przyprostokątnej b narysowana przy kącie prostym,
− dla ctgα strzałka od przyprostokątnej b do przyprostokątnej a narysowana przy kącie prostym,
skierowana odwrotnie jak dla tgα.
Analogicznie rysuję dla kąta β:
− dla sinβ strzałka od przyprostokątnej b do przeciwprostokątnej c, narysowana przy drugim
kącie ostrym − przy kącie α,
− dla cosβ strzałka od przyprostokątnej a do przeciwprostokątnej c, narysowana przy kącie β,
− dla tgβ strzałka od przyprostokątnej b do przyprostokątnej a narysowana przy kącie prostym,
− dla ctgβ strzałka od przyprostokątnej a do przyprostokątnej b narysowana przy kącie prostym,
skierowana odwrotnie jak dla tgβ.
6 mar 00:41
Jakub:

Funkcje trygonometryczne dla kąta α
6 mar 15:19
Jakub:
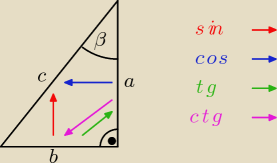
Funkcje trygonometryczne dla kąta β
6 mar 15:44
Gustlik: O właśnie − taki właśnie stosuję schemat. Czy mógłbyś to zamieścić na głównej stronie z
trygonometrii?
6 mar 22:31
Jakub: Na stronie głównej staram się podawać wiadomości w jak najprostszej skondensowanej postaci. Nie
bardzo jest tam miejsce na dwa sposoby liczenia funkcji trygonometrycznych. Jak ktoś będzie
dociekliwy, to zajrzy tutaj.
8 mar 17:08
Agusz: fajna stronka

dobrze, że istnieje ktoś kto zna się na matmie

15 mar 15:52
Dudi: Racja, tu jest super po objaśniane. Dzięki Jakub ^^.
17 kwi 18:58
magda: ale te wzory stosuje się gdy kąt α jest < β

bo kiedy α będzie > od β to będzie on
oznaczony na górze i wtedy α liczymy ze wzoru zgodnego dla kąta β ?
26 kwi 17:54
magda: ale te wzory stosuje się gdy kąt * α jest > β bo kiedy *α będzie < od β to będzie on oznaczony
na górze i wtedy α liczymy ze wzoru zgodnego dla kąta β ?
poprawka
26 kwi 17:55
Jakub: Te wzory są prawdziwe niezależnie czy α<β, czy α>β.
26 kwi 18:10
z II LO: Witam
mam proste pytanie

Czy to bedzie blad jezeli w zadaniu napisze cos30(st.) zamiast sin60(st.)?
Prosze o szybka odpowiedz

27 kwi 17:48
Jakub: Hmm. Jedyne co mogę napisać, że cos30o = sin60o = 12. A czy można dać cos30o zamiast
sin60o? To zależy od zadania.
27 kwi 20:07
zorczarowana:
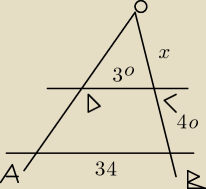
Mam pytanie do twierdzenia Talesa.
Do proporcji...w jednym zadaniu jest trójkąt:
I na lekcji dobieraliśmy proporcje O/C przez C/D równa się C/B przez B/A
Natomiast na korepetycjach dziewczyna uczyła mnie, że O/C przez C/D równa się OC+CB przez B/A
W obu przypadkach wyjdzie inny wynik, teraz nie wiem jak rozwiązywać zadanie...pomóżcie,
proszę.
11 sie 11:57
Jakub: Dziewczyna na korepetycjach ma rację, w szkole robiliście źle. Może nauczyciel się pomylił.
Zapytaj go.
13 sie 16:33
Łukasz1994PZA: Super że to się tutaj znajduje, naprawdę super. Dzisiaj właśnie zacząłem edukację w liceum
(mat−fiz) i Pani nam juz w pierwszy dzień kazała sobie przypomnieć fuckcje i inne pierdoły bo
będzie sprawdzian powtórzeniowy. Ja nic nie pamiętałem więc wpisałem w google i jest.
Elegancko zrobione. Teraz już wszystko wiem o fuckcjach. Coś czuję że dostanę piątkę
<cwaniak2>

2 wrz 18:21
Klaudia: super materiał bardzo mi pomógł

18 paź 15:44
Natala: Jakub! jesteś świetnym nauczycielem

pierwszy raz coś zrozumiałam

Pisałam niedawno sprawdzian z tego działu i nie mogłam uwierzyć w to, że rozwiązałam wszystkie
zadania

może będą ze mnie ludzie?

Wiem jednak, że robiłam jeden błąd: źle odczytywałam z tablicy z miarami kątów sin, cos itd.
Mógłbyś tu wspomnieć, że należy liczby po przecinku zaokrąglać

to na 100% pomoże innym
Dziękuję bardzo za pomoc

i pozdrawiam
14 lis 11:21
Karol: panie Jakubie WAŻNA SPRAWA czy można wytłumaczyć tą tabelkę dlaczego takie liczby a nie inne

15 lis 20:56
Paweł: Przyłączam się do pytania przedmówczyni. Pamiętam że pani profesor narysowała nam dwa trójkąty
i dalej nie wiem co robić.
4 gru 19:45
Jakub: Już jest. Kliknijcie link "obliczanie tych wartości" pod tabelką na poprzedniej stronie.
5 gru 01:50
Januszek75: oznaczenie trojkąta błędne − wierzchołki oznacza się w kierunku przeciwny do wskazówek zegara
8 gru 10:57
sokrates4567: a sec α i cosec α


22 sty 20:56
Ein: Ubóstwiam tę stronę! Można z niej nauczyć się WSZYSTKIEGO do matury! Jakub, naprawdę podziwiam
Cię za ogrom pracy jaki w nią włożyłeś.
22 lut 13:34
szatek: Pomóżcie
Uzasadnij , że nie istnieje kat ostry α taki że sinα+cosα = 5/3
9 mar 13:23
Jakub: sinα + cosα = 53 /()2
(sinα + cosα)2 = 259
sin2α + 2sinαcosα + cos2α = 259
sin2α + cos2α + 2sinαcosα = 259
1 + sin2α = 279
sin2α = 179
Takie równanie nie ma rozwiązania, ponieważ sinus nie ma wartości większych od 1. Z tego
wynika, że pierwsze równanie też nie ma rozwiązania.
2 kwi 01:17
***********: heh strona niezla mam 15 lat a wszystko rozumiem z tego co tu jest w przeciwienstwie do
wikipedi ~~
11 kwi 16:59
marta: kąt α jest ostry i cosα=3/7 wtedy ? sinα? jak to rozwiazac

1 maj 16:09
gimnazjalista: marta ja to policzyłam na kalkulatorze wyszło mi że α ≈ 64,62 stopni
1 maj 19:26
Jakub: Na kalkulatorze to można tylko przybliżoną wartość sinα policzyć. W matematyce trzeba podawać
dokładne wartości. To zadanie najlepiej zrobić jak na
1540.
1 maj 20:20
gimnazjalista: o, faktycznie, super ! trygonometria jest taka ciekawa !
1 maj 23:34
Jaga: Ja mam takie pytanko. Skoro mam daną przyprostokątną naprzeciw kąta i przyprostokątną przy
kącie − mam wyliczyć przeciwprostokątną. To skąd mam wiedzieć czy wybrać tg czy ctg ?
19 maj 11:03
Jaga: Ojej błąd − miało być że wyliczyć przyprostokątną naprzeciw − dana jest przyprotsokątna przy
kącie.
19 maj 11:06
ewela: super stronka


17 sie 12:30
Gustlik: Wymysliłem ostatnio wierszyk do "strzałkowego" schematu obliczania funkcji trygonometrycznych,
opisanego przeze mnie, a narysowanego przez Jakuba:
Sinus − w opozycji,
Cosinus − w koalicji
Tangens − do domu
Cotangens − z domu.
Oczywiście nie są to fachowe definicje funkcji trygonometrycznych, a jedynie "sztuczka
mnemotechniczna" ułatwiająca ich liczenie.
Wierszyk znacznie ułatwia rysowanie strzałek we właściwym miejscu trójkąta i w odpowiednim
zwrocie, zwlaszcza gdy trójkąt jest obrócony, narysowany "krzywo", czyli gdy nie "stoi" na
żadnej z przyprostokątnych. Wielu osobom w takich przypadkach się to miesza, liczą funkcje z
niewłaściwych boków, a za pomocą "schematu strzałkowego" i wierszyka rysują strzałki tam,
gdzie trzeba i we właściwym kierunku i potem wartości funkcji już łatwo obliczyć.
Wyjaśnienie:
Sinus − w opozycji, bo strzałka "biegnie" po "przeciwległym" do danego kącie ostrym,, a więc "
w opozycji" do kąta, którego sinus liczymy,
Cosinus − w koalicji, bo strzałka "biegnie" po danym kącie ostrym, a więc "w koalicji" z kątem,
którego cosinus liczymy,
Tangens − do domu, bo strzałka "biegnie" w stronę kąta, którego tangens liczymy,
Cotangens − z domu, bo strzałka "biegnie" od kąta, którego cotangens liczymy,
16 paź 00:15
:D: może to głupie co napiszę ale myślę ze te trójkąty powinny być narysowane |
\
zadania z matematyki przeważnie pokazują trójkąt w tej pozycji

ale to tylko tak napisałem i tak jest dobrze
16 lis 11:19
daria: ale mi się podoba ta stronka bardzo pomaga

1 sty 19:47
Kamil: bardzo pomocna strona

3 sty 19:17
Uziu: dzięki tej stronie w końcu skończyły się moje problemy z matmą
strona na 6+
brawo dla autora


8 sty 18:38
asdgs: brawwo Jakub Gada
10 sty 11:18
luska: super strona

18 kwi 21:01
kkkasiula: ee to ze strzałkami wymiata nigdy nie mogłam zapamiętać tego no nigdy a tu proszę

22 kwi 17:24
adam: Jakubie czyli sin α i sin β to to samo

/moge liczyc i z tego i ztego

nie rozumiem tego
zbytnio.ja zawsze liczylem z sin,cos,tg,ctg α.po co ta β jest?bardzo prosze o szybka
odpowiedz,zalezy mi na tyum bardzo

5 maj 13:39
Jakub:
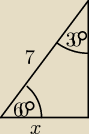
Chodziło mi o to, aby pokazać, że jak masz w trójkącie dwa kąty, tak jak np. na rysunku 60
o i
| | x | | x | |
30o, to można x policzyć zarówno z cos60o = |
| jak i z sin30o = |
| . Dlatego |
| | 7 | | 7 | |
wypisałem też sinβ itd.
Pamiętaj jednak, że to tylko wykorzystanie definicji, które są wyżej. Jak wiesz, że np.
| | przyprostokątna naprzeciw kąta | |
sinus kąta = |
| |
| | przeciwprostokątna | |
to nie ma znaczenia, czy ten kąt to 30
o, 60
o, α, czy β i tak ułożysz właściwą równość.
5 maj 15:39
adam: dzieki wielkie.Juz rozumiem

pozdrawiam.nich Pana trzyma kciuki za mnie i za wszystkich
zdajacych mature

dzisiaj koncze material

5 maj 16:24
Barbadoska : Dzień Dobry. Od Tygodnia zastanawiam sie jak rozwiązac te pożal sie boże zadania i... no nie
potrafię

Może Panu udałoby się zrobić kilka. Z góry dzięki
1) Wyzacz wartość tożsamości kąta α jeśli sin α =
513
2) W trójkącie prostokątnym przeciwprostokątna o długości 4
√2 m, nachylona jest do
przyprostokątnej pod kątem 60 stopni. Ta przyprostokątna ma długość....?
3) Wartość wyrażenia
cos60 stopnisin45 stopni − tg30 stopni =
4) Rozwiąż równanie cos α = sin 45 stopni. Dla α ε (0 stopni ; 90stopni)
5) Kąt α jest ostry i cos α =
1 5 Oblicz 1−2 tg α
6) Dach domu ma kształt trójkąta równoramiennego, którego ramiona mają długość 8m a podstawa
10m. Wyznacz przybliżony kąt nachylenia dachu do płaszczyzny poziomego stropu.
8 maj 15:31
JA ;):
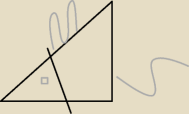
Dla humanistów : spróbujcie popatrzec na kat ja na mysz
od ogona do uszu zawsze jest sinus od dołu do uszu cosinus od ogona do dołu tanges i od dołu
do ogona cotanges
17 paź 09:42
Leopold: Ja jestem wdzięczny niesamowicie, że istnieje taka strona. Zrozumiałem trygonometrię w
czterdzieści minut. Zaoszczędziłem pieniądze.
10 gru 06:10
asia: Dla mnie najlepszym określeniem co to tg , ctg, sin , cos jest ułamek o przy i przeciw
prostokątnych. Nie ma bata, jak to zapamiętasz, to trójkąt może stać nawet do góry "nogami"a
zawsze znajdziesz odpowiednie boki trójkąta do przeciwległego kata

Dzięki Jakubie !
21 lut 19:10
adam: suuuuper stronka. Uwielbiam Pana Jakuba
6 mar 17:40
adam: liczba sin
245
0 równa jest liczbie
A= cos45
0 B= cos60
0 C= tg45
0 D= tg60
0
proszę o odpowiedź i rozwiązanie

6 mar 20:07
Bartecki: Dzięki ci wielkie,dzięki tej stronie 5 wpadła

20 mar 19:31
lililibi:
DZIĘKUJE<3
Tylko jeszcze, mam pytanie.
Co jesli mam jedną niewiadomą ? Wiem, że do tego używa sie Pitagorasa.. ale w jaki sposob?
16 cze 19:02
Jakub: Z jedną niewiadomą jest po prostu łatwiej dobrać odpowiednią funkcję trygonometryczną, aby
policzyć tą niewiadomą.
16 cze 23:37
Zdezorientowana: Jakubie, mam problem, skąd mam wiedzieć kiedy mam wybrać sin czy cos itd?nie rozumiem....
9 paź 17:28
W: Brawo, znakomita strona!
13 sty 22:48
Arleton: ctg nie ma na podstawowej maturze
9 mar 11:40
Jakub: Nie ma. Jednak kiedyś było i jeszcze w niektórych szkołach uczą, dlatego dodałem.
9 mar 15:08
krejman: Mógłby mi ktoś wytłumaczyć dlaczego sin α dla α równej 90 stopni wynosi 1?
29 mar 20:29
littleMi: wydaje mi sie ze pomyliliscie oznaczenia a i b a powinno byc na dole a b z boku. przy kazdym
zadaniu ktore rozwiazuje cos jest nie tak. ogolnie zadania super bardzo pomagaja. pozdrawiam
30 kwi 12:32
Jakub: Nie ma znaczenia jak są ułożone a, b na rysunku. Ważne, aby na ich podstawie poprawnie układać
wzoru według reguł np.
| | długość przyprostokątnej naprzeciwko α | |
sinα = |
| |
| | długość przeciwprostokątnej | |
30 kwi 18:50
KOMAR: Proponuję podanie uczniom takiego ciągu dla wartości funkcji sinus z pierwszej ćwiartki
0 30 45 60 90
√0 √1 √2 √3 √4
sinα −−−−− −−−−− −−−−− −−−−− −−−−−
2 2 2 2 2
resztę można sobie wyprowadzić
25 sie 11:06
OjciecMaPojutrzeSprawdzian:
Pierwiastek z Matki wszystkich dobroci......dzięki!
...się dowiedziałem się, że mam tłumaczyć bo "nie rozumie wszystkiego", beton zbrojony

18 paź 20:43
 Funkcje trygonometryczne dla kąta α
Funkcje trygonometryczne dla kąta α
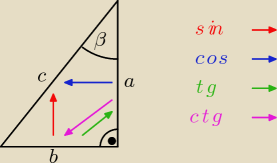 Funkcje trygonometryczne dla kąta β
Funkcje trygonometryczne dla kąta β
 dobrze, że istnieje ktoś kto zna się na matmie
dobrze, że istnieje ktoś kto zna się na matmie 
 bo kiedy α będzie > od β to będzie on
oznaczony na górze i wtedy α liczymy ze wzoru zgodnego dla kąta β ?
bo kiedy α będzie > od β to będzie on
oznaczony na górze i wtedy α liczymy ze wzoru zgodnego dla kąta β ?
 Czy to bedzie blad jezeli w zadaniu napisze cos30(st.) zamiast sin60(st.)?
Prosze o szybka odpowiedz
Czy to bedzie blad jezeli w zadaniu napisze cos30(st.) zamiast sin60(st.)?
Prosze o szybka odpowiedz 
 Mam pytanie do twierdzenia Talesa.
Do proporcji...w jednym zadaniu jest trójkąt:
I na lekcji dobieraliśmy proporcje O/C przez C/D równa się C/B przez B/A
Natomiast na korepetycjach dziewczyna uczyła mnie, że O/C przez C/D równa się OC+CB przez B/A
W obu przypadkach wyjdzie inny wynik, teraz nie wiem jak rozwiązywać zadanie...pomóżcie,
proszę.
Mam pytanie do twierdzenia Talesa.
Do proporcji...w jednym zadaniu jest trójkąt:
I na lekcji dobieraliśmy proporcje O/C przez C/D równa się C/B przez B/A
Natomiast na korepetycjach dziewczyna uczyła mnie, że O/C przez C/D równa się OC+CB przez B/A
W obu przypadkach wyjdzie inny wynik, teraz nie wiem jak rozwiązywać zadanie...pomóżcie,
proszę.


 pierwszy raz coś zrozumiałam
pierwszy raz coś zrozumiałam  Pisałam niedawno sprawdzian z tego działu i nie mogłam uwierzyć w to, że rozwiązałam wszystkie
zadania
Pisałam niedawno sprawdzian z tego działu i nie mogłam uwierzyć w to, że rozwiązałam wszystkie
zadania  może będą ze mnie ludzie?
może będą ze mnie ludzie?  Wiem jednak, że robiłam jeden błąd: źle odczytywałam z tablicy z miarami kątów sin, cos itd.
Mógłbyś tu wspomnieć, że należy liczby po przecinku zaokrąglać
Wiem jednak, że robiłam jeden błąd: źle odczytywałam z tablicy z miarami kątów sin, cos itd.
Mógłbyś tu wspomnieć, że należy liczby po przecinku zaokrąglać  to na 100% pomoże innym
Dziękuję bardzo za pomoc
to na 100% pomoże innym
Dziękuję bardzo za pomoc  i pozdrawiam
i pozdrawiam






 ale to tylko tak napisałem i tak jest dobrze
ale to tylko tak napisałem i tak jest dobrze






 /moge liczyc i z tego i ztego
/moge liczyc i z tego i ztego nie rozumiem tego
zbytnio.ja zawsze liczylem z sin,cos,tg,ctg α.po co ta β jest?bardzo prosze o szybka
odpowiedz,zalezy mi na tyum bardzo
nie rozumiem tego
zbytnio.ja zawsze liczylem z sin,cos,tg,ctg α.po co ta β jest?bardzo prosze o szybka
odpowiedz,zalezy mi na tyum bardzo
 Chodziło mi o to, aby pokazać, że jak masz w trójkącie dwa kąty, tak jak np. na rysunku 60o i
Chodziło mi o to, aby pokazać, że jak masz w trójkącie dwa kąty, tak jak np. na rysunku 60o i
 pozdrawiam.nich Pana trzyma kciuki za mnie i za wszystkich
zdajacych mature
pozdrawiam.nich Pana trzyma kciuki za mnie i za wszystkich
zdajacych mature dzisiaj koncze material
dzisiaj koncze material
 Może Panu udałoby się zrobić kilka. Z góry dzięki
1) Wyzacz wartość tożsamości kąta α jeśli sin α = 513
2) W trójkącie prostokątnym przeciwprostokątna o długości 4√2 m, nachylona jest do
przyprostokątnej pod kątem 60 stopni. Ta przyprostokątna ma długość....?
3) Wartość wyrażenia cos60 stopnisin45 stopni − tg30 stopni =
4) Rozwiąż równanie cos α = sin 45 stopni. Dla α ε (0 stopni ; 90stopni)
5) Kąt α jest ostry i cos α = 1 5 Oblicz 1−2 tg α
6) Dach domu ma kształt trójkąta równoramiennego, którego ramiona mają długość 8m a podstawa
10m. Wyznacz przybliżony kąt nachylenia dachu do płaszczyzny poziomego stropu.
Może Panu udałoby się zrobić kilka. Z góry dzięki
1) Wyzacz wartość tożsamości kąta α jeśli sin α = 513
2) W trójkącie prostokątnym przeciwprostokątna o długości 4√2 m, nachylona jest do
przyprostokątnej pod kątem 60 stopni. Ta przyprostokątna ma długość....?
3) Wartość wyrażenia cos60 stopnisin45 stopni − tg30 stopni =
4) Rozwiąż równanie cos α = sin 45 stopni. Dla α ε (0 stopni ; 90stopni)
5) Kąt α jest ostry i cos α = 1 5 Oblicz 1−2 tg α
6) Dach domu ma kształt trójkąta równoramiennego, którego ramiona mają długość 8m a podstawa
10m. Wyznacz przybliżony kąt nachylenia dachu do płaszczyzny poziomego stropu.
 Dla humanistów : spróbujcie popatrzec na kat ja na mysz
od ogona do uszu zawsze jest sinus od dołu do uszu cosinus od ogona do dołu tanges i od dołu
do ogona cotanges
Dla humanistów : spróbujcie popatrzec na kat ja na mysz
od ogona do uszu zawsze jest sinus od dołu do uszu cosinus od ogona do dołu tanges i od dołu
do ogona cotanges
 Dzięki Jakubie !
Dzięki Jakubie !


