mam problema: a jak jest −7x³ no i za x wstawimy np. −2 to będzie (−7)(−8)=56 to to jak to bedzie −∞? ja wiem ze Ty masz dobrze ale mnie interesuje jak do tego dojść, bo za x jak weźmiemy liczby dodatnie to wiem ze wyjdzie −∞ ale jak weźmiemy za x liczby ujemne to jakos nie widze tego ciągu, granicy

Jakub: Tam jest x → + ∞, pod lim. Oznacza, to że wprawdzie możesz zacząć od −2, ale prędzej czy później musisz zacząć brać liczby rozbieżne do +∞. One będą dawał wartości −7x³ rozbieżne do −∞. x: −2 0 1 10 → +∞ −7x³: 56 0 −7 −7000 → −∞ Dlatego lim_x→+∞ (−7x³) = −∞

mam problema: aaaaaa, no teraz to rozumiem skąd ten −∞, ale znowu nie rozumiem co to znaczy ze coś jest zbieżne czy rozbieżne

ich: rozbieżne − granica +/− ∞ zbieżne − granica w konkretniej liczbie np. 3

anonim: lim_x→+∞ 7/x³ = 0 Tak jest dlatego że wynik 'zmierza' do zera? Jeśli pod x podstawię 1 to da nam 7, następnie podstawię np. 2 i wynik będzie niższy, bo 7/8. O to w tym chodzi?

Jakub: Dokładnie. Jak będziesz podstawiał pod x coraz większe liczby, bo x→+∞, to będziesz otrzymywał coraz mniejsze ułamki. Kolejne ułamki będą coraz bliższe zero, więc wynik granicy to zero.

Liroy: Nie wiem dlaczego lim_x→+∞ e^−1₂x2=∞ Prosze o wyjasnienie.

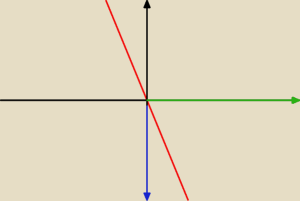
Patryk: lim_x→∞(−2x)=−∞ Czy gdybym chciał to graficzne przedstawić to było by tak ? f(x)=−2x lim_x→∞(−2x)=−∞ −2x ← ta nasza funkcja x→∞ ← oś ox (argumentów) −∞ ← wartosci z osi oy

Patryk: ?

Jakub: Dokładnie Na wykresie f(x) = −2x wyraźnie widać, jak dla x → +∞ wartości są rozbieżne do −∞.

Patryk: Czyli jest tak jak myślałem , dzięki ,ze mnie upewniłeś ,tylko w ten sposób to zrozumiałem

jogurt: @mam problema ale (−2)³ to −8 więc dalsze rozumowanie jest błędne liczba ujemna do potęgi nieparzystej pozostaje ujemną