matematyk:): takich rzeczy nie będzie nawet na rozszerzeniu?

Jakub: Link do poprzedniej strony jest zaznaczony na czarno, co oznacza, że to jest materiał spoza liceum. Inna sprawa, że łatwo się tego nauczyć i warto.

Emil : u mnie w LO taki materiał jest normalnie prowadzony na lekcji

Raison: Przecież może być też ciąg naprzemienny. Jeśli jest ciąg geometryczny a q<0 ... lub stały jeśli q=1... lub dla arytmetycznego jeśli r=0 ... No ale nic Swoją drogą świetna stronka. Jeśli czegoś nie rozumiem, zawsze tu zaglądam i wszystko staje się jasne Pozdrawiam

Jakub: Tytuł tej strony jest "monotoniczność ciągu", więc nie obejmuje tego, co napisałeś Raison.

hop...: u mnie też jest to w programie, a mam matme podstawową. To jest po prostu obowiązkowe.

Daniel : Dlaczego tam 1,3,5,7 an= 2n−1 a nie tylko 2n ?

Daniel : Aha dobra już wiem

Milu: u mnie też jest obowiązkowe, jak wiele rzeczy materiału oznaczonego "ze studiów"

wampa: a wam się nudzi ? Mam pytanie; bawię się liczbami i natrafiłem na problem; jak policzyć sumę ciągu określonego wzorem aⁿ ?

Wojtek: podobno monotoniczność można obliczyć też z tego czy to prawda?

an+1
	>1 ciag rosnący
an

an+1
	<1 ciąg malejący
an

Jakub: @wampa To mi wygląda na sumę ciągu geometrycznego. Zobacz 279. @Wojtek W zasadzie tak. Problem jest, gdy niektóre wyrazy ciągu są równe zero. Przez zero nie wolno dzielić i dla takich wyrazów tej definicji nie zastosujesz. Jednak jak masz pewność, że wszystkie wyrazy ciągu są różne od zera, to możesz jej używać.

Gustlik: Monotoniczność niektórych ciągów można badać wykorzystując własności odpowiednich funkcji i nieraz tak jest łatwiej i bardziej obrazowo. Ta metoda odnosi się do ciągów podanych wzorem łatwej do zbadania funkcji, np. liniowej, kwadratowej, wykładniczej czy homograficznej. Wystarczy napisać wzór funkcji zastępując we wzorze ciągu "n" "x"−em, a "a_n" "y"−em, potem np. narysować wykres (niekiedy wystarczy przybliżony) danej funkcji i odczytać z wykresu, jak zachowuje się ta funkcja dla liczb naturalnych dodatnich. W przypadku niektórych ciągów i funkcji można monotoniczność odczytać ze wspólczynników występujących we wzorze ciągu (np. funkcja liniowa, wykładnicza oraz homograficzna po sprowadzeniu do postaci kanonicznej). Np. a_n=4n+3 będzie rosnący, bo funkcja y=4x+3 jest rosnaca (współczynnik kierunkowy a=4 jest dodatni), a_n=2ⁿ też jest rosnący, bo funkcja y=2^x jest rosnaca (podstawa potęgi>1),

	2		2
an=		+3 jest malejący, bo funkcja y=		+3 też jest malejąca itp.
	n		x

Oczywiście warto znać oba sposoby, bo nie każdy ciąg da sie zapisać wzorem łatwej do zbadania funkcji, np. a_n=(n+2)! albo a_n=n³+5n²−3n+4, w tym drugim przypadku mozna byłoby sobie pomóc funkcją, niemniej trzeba znać pochodne, bo wielomian nie jest już tak łatwy do zbadania jak np. funkcja kwadratowa.

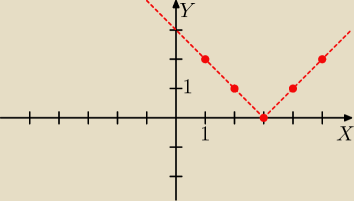
Gustlik: Przykład ciągu, który można zbadać łatwiej funkcją, niż metodą "a_n+1−a_n" a_n=|n−3| Rysujemy wykres funkcji y=|x−3| i nanosimy na wykres punkty odpowiadające kolejnym wyrazom tego ciągu. Z rysunku widać wyraźnie, że ciąg jest niemonotoniczny, bo dla wyrazów a₁, a₂, a₃ jest malejący, a od a₃ rosnący. Badanie tego ciagu metoda rachunkową byłoby dość kłopotliwe z uwagi na konieczność stosowania definicji wartości bezwzględnej i odpowiednich założeń.

Kate: muszę równiez zauważyć, że jest to materiał z podstawy,

Mateusz: @Wampa jesli ciąg jest skonczony wtedy jego suma wynosi: n

	xn+1−1
∑ xk=
	x−1

k=0 jesli natomiast suma jest nieskonczona i |x|<1 wtedy: ∞

	1
∑ xk=
	1−x

k=0

2 liceum, nowa podstawa: Od tego roku monotonicznosc jest juz na maturze, przynajmniej na rozszerzeniu.

quarhodron: Gustlik świetna rada ! Jakoś na to nie wpadłem, ze tak można i zawsze z definicji wyznaczałem. Dzięki wielkie, to często upraszcza wiele rzeczy

gościu221: co do oznczeń akresu materiału, w liceum też on obowiazuje, do matury rozszerzonej.

Avatar: Z tego co mi wiadomo to na podstawie w liceum też to jest jako obowiązkowe.

Jakub: W standardach maturalnych nic nie ma o monotoniczności ciągu na podstawie. Nie przypominam sobie też ani jednego zadania maturalnego z tego tematu. Raczej tego nie ma na podstawie. Piszę raczej, bo standardy są nieprecyzyjne i nie można z całą pewnością powiedzieć, że zadanie z monotoniczności ciągu nie będzie na maturze podstawowej.