Wera: w końcu strona z porządnymi , przejrzystymi objaśnieniami

samuraj: My na lekcjach określaliśmy monotoniczność wyliczając ją np: f(x)=4−x założenie x2−x1>0 f(x2)−f(x1)=4−x2−(4−x1)=4−x2−4+x1=−x2+x1=−(x2−x1) funkcja malejąca I trochę tego nie rozumiem właśnie.

Jakub: Ja napisałem x₁ < x₂, co po przekształceniu x₁ < x₂ 0 < x₂ − x₁ x₂ − x₁ > 0 daje twoje x₂−x₁>0. Tak więc początkowe założenie u mnie i u ciebie jest takie samo. Następnie sprawdzacie znak różnicy f(x₂)−f(x₁) = ... = −(x₂−x₁) < 0 (bo x₂−x₁>0) czyli f(x₂)−f(x₁) < 0 f(x₂) < f(x₁) f(x₁) > f(x₂) Zgodnie z definicją na poprzedniej stronie jest to funkcja malejąca. Dobrze robicie w klasie. Jak czegoś jeszcze nie rozumiesz to pytaj.

moni30003: Już teraz rozumiem, dzięki.

Anka: a u mnie ucza czegoś takiego jak: funkcja nierosnąca x1 < x2 to f(x1) ≥ f(x2) funkcja niemalejąca x1 < x2 to f(x1) ≤ f(x2) Jakub o co w tym chodzi

Jakub: Twoje definicje są podobne, do tego co ja napisałem, tylko uwzględniają też funkcję stałą. Wyobraź sobie wykres funkcji, który rośnie później przechodzi w stałą, a później znowu rośnie. W pewnym przedziale jest stały, a w pozostałych rosnący. To jest właśnie funkcja niemalejąca. Funkcja nierosnąca to funkcja stała lub malejąca. f(x1) ≥ f(x2) − oznacza, że wartości po lewej (dla x₁) są większa lub równe dla wartości po prawej (dla x₂). Funkcja niemalejąca to funkcja stała lub rosnąca f(x1) ≤ f(x2) − oznacza, że wartości po lewej (dla x₁) są mniejsze lub równe dla wartości po prawej (dla x₂). To co napisałem, spróbuj sobie wyobrazić na wykresach z 26.

Aśka: Musze przyznać że jestem osioł z matematyki i w ząb nic nigdy nie kumałam, a tu nagle wchodzę na twoją stronkę i wszystko rozumiem co objaśniasz fajnie i przejrzyście jestem zachwycona też twoją stroną i doceniam w niej też wygląd strony zresztą zachęcający do wchodzenia częściej bo jestem właśnie na kierunku informatycznym serdecznie pozdrawiam i oby tak dalej gratuluję swietnych wyników twojej pracy

Marta: tu sa zle definicje

Jakub: Definicje są dobre. Umiesz uzasadnić bardziej swoje twierdzenie, niż tylko napisać, że definicje są złe?

Gosia: dziękuje bardzo mi to pomogło w przypomnieniu. pozdr

Ewka : jak w sposób algebraiczny okreścić monotoniczność funkcji f(x)=^x+1_x−5 ? liczę f(x₁) − f(x₂) i po przekształceniach dostaję ^{−6(x₁−x₂)}_{(x1−5)(x2−5)} co z tym dalej zrobić? z definicji wynika, że jeśli x₁−x₂ <0 to −6(x₁ − x₂) będzie dodatnie a co z mianownikiem?

Jakub: Dalej rozbijasz na dwa przedziały, bo 5 nie należy do dziedziny 1. dla x₁<5, x₂<5 i x₁−x₂<0 masz −6(x₁−x₂) > 0, x₁−5<0, x₂−5<0 czyli

	−6(x1−x2)
f(x1) − f(x2) =		>0
	(x1−5)(x2−5)

f(x₁) > f(x₂) funkcja malejąca w przedziale (−∞,5) 2. dla x₁>5, x₂>5 i x₁−x₂<0 masz −6(x₁−x₂) > 0, x₁−5>0, x₂−5>0 czyli

	−6(x1−x2)
f(x1) − f(x2) =		>0
	(x1−5)(x2−5)

f(x₁) > f(x₂) funkcja malejąca w przedziale (5,∞)

	x+1
Funkcja f(x) =		jest malejąca w przedziałach (−∞,5) i (5,∞), ale w całej swojej
	x−5

dziedzinie nie jest malejąca. W całej swojej dziedzinie jest niemonotoniczna.

	x+1		x−5+6		x−5		6		6
Wykres f(x) =		=		=		+		= 1 +
	x−5		x−5		x−5		x−5		x−5

jest trochę podobny do tego na 169.

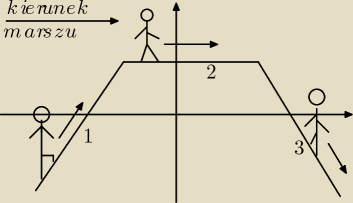
Gustlik: Najbardziej obrazowa metoda odczytywania monotoniczności funkcji z wykresu: Wyobrazić sobie, że wykres funkcji przedstawia ukształtowanie terenu, np. profil szlaku turystycznego, a my "maszerujemy" po tym terenie w prawo, tj. w stronę dodatniej półosi OX. Jeżeli idziemy pod górę, to funkcja rośnie, jeżeli idziemy w dół, to funkcja maleje, a jak idziemy po równym poziomym terenie to funkcja stała. Na rysunku: 1 − funkcja rosnąca 2 − funkcja stała 3 − funkcja malejąca

Maciek: Witam, jestem zachwycony stronką Pozdrawiam prowadzącego i liczę na pomoc. Dla funkcji rosnącej : Rachunkowo: f(x) = 2x+3 f(x₁) − f(x₂) = (2x₁+3) − (2x₂+3) = 2x₁ + 3 − 2x₂ − 3 = 2(x₁−x₂) Jak ten przykład będzie wyglądał dla funkcji malejącej? Pozdrawiam.

Jakub: Podobnie. Przykładowo dla f(x) = −2x+3 Jeżeli x₁ < x₂ to f(x₁) − f(x₂) = (−2x₁+3) − (−2x₂+3) = −2x₁+3+2x₂−3 = −2x₁+2x₂ = −2(x₁−x₂) > 0. f(x₁) − f(x₂) > 0 f(x₁) > f(x₂) funkcja malejąca

Maciek: Witam raz jeszcze. Bardzo dziękuję za wyjaśnienie funkcji malejącej. Nie umiem się odnaleźć na forum. Dlatego mam takie pytanie: Zbadaj monotoniczność funkcji: x²−3, x nalezy do Rzeczywistych ujemnych POMOCY ! ! !

Jakub: Dlaczego nie umiesz się odnaleźć na forum?

tsjulius: do Marty słowo "najczęściej" użyte przez Jakuba w pierwszym wersie załatwia sprawę. Zapewne miałaś na myśli funkcje nierosnące i niemalejące. Rzeczywiście funkcje monotoniczne to takie, które są albo rosnące, albo malejące, albo nierosnące, albo niemalejące. Ale to strona dla maturzystów i na poziomie podstawowym wystarczy pojęcie funkcji stałej − czyli takiej, która jednocześnie jest nierosnąca i niemalejąca. Rozszerzenie to co innego. Ale i tak na ogół oczekuje się na maturze określania monotoniczności funkcji przedziałami. Nawet na rozszerzeniu.

kaszucha: W opisie funkcji malejącej jest błąd − znak się nie zgadza Pozdrawiam

Jakub: Znak się zgadza. Zobacz na wykres.

Miki: witam. Mam pytanie czy określając przedziały funkcji rosnącej piszemy przedział zamknięte, czy otwarty. ? Spotykam się z różnymi wersjami.