Ania: Polecenie jest bez sensu, gdyż w treści zadania jest już podany obwód. Zamiast polecenia:"Oblicz jego obwód i pole" powinno się znajdować, np.: "Oblicz długości boków trójkąta i jego pole"

Jakub: Treść zadania sprawdza, czy wiesz, co to jest obwód − suma długości boków. Tak jak napisałaś jest łatwiej, ale w zadaniach z matematyki nie chodzi o to, aby było łatwo.

Adam: Dokładnie − W zadaniu został podany obwód, a w poleceniu jego obliczenie... Pozdrawiam : )

Jakub: Oczywiście macie rację. W sumie to sam nie rozumiem, o co mi chodziło, jak odpowiadałem Anii

Piotr: A nie można wykorzystać właściwości trójkąta egipskiego? Ma boki o długości 3,4,5 a obwód 12.

	120
Jeżeli w zadaniu ma być trójkąt o obwodzie 120 to wystarczyłoby policzyć skalę (		=10)
	12

i przemnożyć przez nią każdy bok ( (3+4+5)*10 = 120). Moim zdaniem jest to łatwiejszy sposób.

Jakub: Też dobry sposób. Tylko nie każdy wie, co to jest trójkąt egipski.

Archimedes: z twierdzenia Pitagorasa (a+2r)² = a²+(a+r)² = a²+a²+2ar+r² po uporządkowaniu −a²+2ar+3r²=0 Wiemy, że obwód a+a+r+a+2r=120, więc 3a+3r=120/:3 a+r=40 => [P[a=40−r] wracając do równania kwadratowego mamy −(40−r)² + 2*(40−r)*r + 3r² = 0 −(1600−80r+r²)+(80−2r)*r + 3r² = 0 −r² + 80 r − 1600 −2r² + 80r +3r² = 0 160r = 1600 /:160 r=10 podstawiając do pogrubionego równania a=40−10 a=30 Proszę powiedzieć, czy jest to poprawnie wykonane zadanie (oczywiście nie całe, tylko do tego momentu, w którym wyliczyłem różnicę i pierwszy wyraz ciągu). a = a₁, dla uproszczenia nie pisałem tej jedynki w indeksie dolnym. Mam nadzieję, że przy przepisywaniu z kartki się nie pomyliłem Pozdrawiam

Archimedes: *errata w momencie "podstawiając do pogrubionego równania" ciężko je zauważyć, ponieważ nie udało mi się go pogrubić i jest zapisane w formie [P[a=40−r] i brakuje jednego nawiasu kwadratowego aby było a=40−r niestety komputery są nieubłagalne

Jakub: To jest poprawne rozwiązanie Archimedes. Trochę krótsze od mojego, ale w sumie podobne.

Rumcajs: Witam. a byłby ktoś w stanie mi podpowiedzieć jak ustaliliście że boki trójkąta mają takie a nie inne miary na rysunku mowa o. 1 bok = a 2 bok= a +r 3 bok= 2a+r skąd te oznaczenia? bo coś się pogubiłem.. nie to że nie znam wzorów ale coś nie zrozumiałem tego do końca.

Rumcajs: Poprawka: przyprostokątna= 1 = a przyprostokątna= 2 = a+r przeciwprostokątna= a+2r

Jakub: W treści zadania masz, że boki trójkąta tworzą ciąg arytmetyczny. Zobacz 264. Oznacza, to że każdy kolejny bok jest o stałą liczbę (r − różnica ciągu arytmetycznego) większy. Najkrótszy bok oznaczyłem jako "a", następny jako "a+r" i największy jako "a+r+r = a+2r". W ten sposób tworzy się ciąg arytmetyczny. Dodając stałą liczbę np. 5, 7, 9, 11, 13, ...

Rumcajs: Panie Jakubie. Dziękuję za wytłumaczenie mi tego. teraz już rozumiem

Roland: Czy to też jest zadania z jakiejś matury próbnej ? Ogl to proste wydają się te zadania z ciągów. PS. Panie Jakubie wielkie dzięki za stworzenie tej stronki, jest bardzo przydatna.

Jakub: To zadania akurat nie było na żadnej maturze. Jednak jest dość popularne w zbiorach w tym dziale.

Gustlik: Prościej tak − ze wzoru na sumę ciągu:

	a1+a3
Obw=a1+a2+a3=		*3=a2*3 (średnia arytm. z wyrazów a1 i a3 wynosi a2)
	2

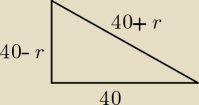
a₂*3=120 /:3 a₂=40 i diabli biorą układ równań, robi się JEDNA niewiadoma. Z Pitagorasa: (40+r)²=(40−r)²+40² 1600+80r+r²=1600−80r+r²+1600 − otrzymuje takie samo równanie, jak u Jakuba, ciąg dalszy więc będzie taki sam. Czyli r=10, zatem a₁=40−10=30, a₃=40+10=50 cm

	1
P=		*40*30=600 cm2
	2

WAŻNE ! Jeżeli w ciągu arytmetycznym mamy dwa wyrazy oba o parzystych numerach albo oba o nieparzystych numerach, to mozna bardzo łatwo obliczyć numer środkowego wyrazu

	a3+a7
(i potem sam wyraz) na zasadzie średniej arytmetycznej, np.		=a5,
	2

	a2+a6		a1+a3
		=a4 itd. Tak samo		=a2 i z tego skorzystałem.
	2		2

UWAGA! Tej metody nie można wykorzystać, gdy mamy jeden wyraz o parzystym numerze, a drugi o nieparzystym, bo średnia wyjdzie ułamkowa, np. gdy będziemy mieli a₃ i a₆, to środkowy wyraz byłby a_4,5, a takiego wyrazu nie ma.

Maszina: Jakubie... Takie przepiękne wyniki mi wyszły, a Ty mi tu robisz zamieszanie Czy ktoś z was może mi powiedzieć, czemu nie mogę tego zrobić tak: a₃ − przeciwprostokątna

	a1 + a3
S3=120=		* 3
	2

(skracając) 80 = a₁ + a₂ potem ładnie wpasowujemy: 120 = a₁ + a₂ + a₃ 120 = a₁ + 80 a₂ = 40 i teraz utworzyłam sobie ciąg: a₁=10, a₂=40, a₃ = 70. Czy suma wyrazów = 120? Tak! Czy jest ciąg arytmetyczny? Jest! r = 30 P=¹₂a₁ * a₂ = ¹₂ 10 * 20 = 200

Maszina: Po przerwie na lody pistacjowe zakumałam o co chodzi. Te proporcje trójkątna prostokątnego po prostu muszą się zgadzać z twierdzeniem Pitagorasa.

Jakub: Dokładnie. Korzystam z twierdzenia Pitagorasa.