o l a: do tego zadania jest zły rysunek, ponieważ środek okręgu opisanego na trójkącie rozwartokątnym leży poza trójkątem a z tego wynika ze suma kątów trójkąta wynosi 360 stopni

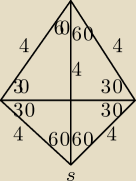
o l a: oto poprawny rysunek

Jakub: Dzięki za informację. Już poprawiłem rysunek.

Paweł: żeby znaleść punkt padania wierzchołka na płaszczyzne podstawy można wykreślić symetralne boków tak jakbyśmy szukali okręgu opisanego na tym trójkącie? czy ten wierzchołek w tym akurat miejscu wziął się z czego innego?

Mastah: Proste zadanie, ale jakoś strasznie pokomplikowane. Trochę niejasny jest rysunek trójkąta równoramiennego, bo nagle 2√3 się pojawiają. A co do obliczenia odcinka AB i h nie lepiej po prostu z sinusa i cosinusa 30 stopni to obliczyc?

kasia: rysunek nadal jest zły

Ateloiw: Skąd wiadomo, że wysokośc pada poza trójkątem? Wynika to z jakiś własności trójkąta równoramiennego?

Jakub: Można policzyć długość odcinka CS z trójkąta CSW.

	|CS|
cos60o =
	|CW|

	|CS|
12 =
	8

|CS| = 4cm Wysokość h trójkąta ABC liczyłem na poprzedniej stronie i wyszła równa 2cm. Wniosek taki, że wysokość pada poza podstawą. Oczywiście czytając zadanie, trudno to sobie wyobrazić. Nie jest to jednak takie ważne. Z wysokością padającą w środku podstawy też da się poprawnie policzyć objętość ostrosłupa. @Mastah usunąłem 2√3 z rysunku. Faktycznie podawanie na rysunku tego, co jest dopiero później liczone, nie jest za dobrym pomysłem.

Monika: Nachylenie do podstawy niczym się nie różni z nachyleniem do krawędzi? Wydaje mi się zaznaczenie kąta 60 stopni oraz kąta prostego niepoprawne. A może jest taka własność?

Jakub: Najczęściej nachylenie do krawędzi ma inny kąt niż nachylenie do podstawy. Na rysunku ostrosłupa nigdzie nie ma nachylenia do krawędzi. Kąty 60^o i 90^o to kąty między krawędzią a powierzchnią podstawy. Dla ułatwienia dorysowałem szare odcinki SA, SB, SC, które w rzeczywistości są promieniami okręgu opisanego na trójkącie ABC.

Krysio: nie lubię tego zadania :<

Arni: Świetny rysunek z widocznymi ścianami bocznymi ,wszystko ładnie i fajnie zrobione !

Kate: nie rozumiem

fasola: Wszysko fajnie i logicznie rozpisane, czasami jest tylko klopot zeby ,,ugryzc,, takie zadanie. Dalej juz leci samo. Fajna stronka pozdrawiam

anon: nie rozumiem, czemu tam jest dodany punkt s?

anon: Kurcze, już zrozumiałem to zadanie Nie mogłem sobie wyobrazić jak to możliwe że środek okręgu opisanego na trójkącie jest po za tym trójkątem

anon: Tak dla pewności jeszcze takie małe pytanko Ten ostrosłup jest pochylony tak bardzo że po prostu wysokość nie pada wewnątrz podstawy(trójkąta równoramiennego).

anon: i pytanie czemu to nie jest ostrosłup pochyły, jeżeli jego spodek jest po za podstawą(trójkątem równoramiennym)?

Jakub: Tak, ten ostrosłup ma tak pochylone ściany boczne, że spodek wysokości jest poza podstawą (trójkątem równoramiennym). Pamiętam, że jak rozwiązywałem to zadanie, to mój pierwszy rysunek był z wysokością padającą wewnątrz trójkąta w podstawie. Jednak jak zacząłem liczyć, to wyszło, że to tak nie może wyglądać i musiałem narysować nowy rysunek. Prawdę powiedziawszy zbyt często nie spotykam się z pojęciem ,,ostrosłup pochyły''. Graniastosłup pochyły tak 986, ale nie ostrosłup pochyły. Aż musiałem poguglać, aby się upewnić. Według tej strony http://studianet.pl/kursy/kreska/rodzaje_wieloscianow.htm w ostrosłupie pochyłym wysokość nie pada na środek okręgu opisanego na podstawie. Tak więc ostrosłup z zadania nie jest pochyły (jest prosty), ponieważ jego wysokość pada na środek okręgu opisanego na podstawie. A że ten środek okręgu jest poza trójkątem, to no cóż jak już sam wiesz, to się zdarza.

gość11111: Czy to zadanie jest na poziom matury podstawowej?

Jakub: Tak, ale z tych trudniejszych.

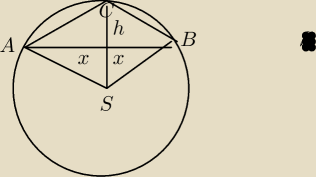
Robert de Clair: po wpisaniu tego trójkąta w okrąg wyszło mi, że wpisany trójkąt A B C jest odbiciem trójkąta A S B, gdzie S jest środkiem tego okręgu (przypadek, czy celowo tak zrobiono dane do tego zadania? a może błąd w mojej kostrukcji) no ale lecimy dalej: Skoro AS = BS = CS to CS:2 (czyli promień/2) = wysokość trójkąta ABC (i ACS) z Sin60' i Cos60' wiemy, że H = 4√3 a odc CS=4 H = 4√3 boki trójkątów = AC, BC, AS, BS = 4 h=1/2 * AC, BC, AS, BS = 2 długość podstawy: (wysokość h dzieli trójkąt równoramienny na 2 trójkąty prostokątne) x²+h²=4² x²+4=16 x²=16−4=12 x=√12 = 2√3 czyli mamy połowę podstawy długość podstawy 2*2√3 czyli 4√3 Wyszliśmy na te same dane więc reszta bez zmian: Pp=(a*h)/2 = 2*4√3 / 2 = 4√3 cm² V=(Pp*H)/3 = (4√3*4√3)/3 = 16*3 / 3 = 16 cm³ Cały czas mam jednak jakieś mgliste przeświadczenie, że gdzieś popełniam błąd w myśleniu. Poprawcie mnie, jeśli mój tok rozumowania jest błędny, albo właściwy tylko dla tego jednego zadania a w innym podobnym już się nie sprawdzi. I np zmiana danych (np kąta podstawy, czy kątów lub długości krawędzi) spowoduje niemożność rozwiązania tego zadania w ten sposób lub co gorsza w sposób podany przez Jakuba.