grzyyb: Pytanie mam, gdy obliczamy juz tgα, to dlaczego "a" zamienia sie w jedynke ?

Jakub: Skracam przez "a" czyli dzielę licznik i mianownik przez "a". a : a = 1 a√2 : a = √2

olka: jakub jestes mistrzem

jjj: dlaczego d to nie apierwiastek3 ?

jjj: przepraszam,juz wiem bo to tg,przeciez

asia: Czy w poleceniu nie ma błędu? to jest kąt między przekątną sześcianu a przekątna ściany bocznej a nie kąt między przekątną sześcianu a ścianą boczną bo to różnica.

Jakub: Jak chcesz narysować kąt między przekątną a ścianą, to musisz narysować rzut prostokątny tej przekątnej na ścianę. Tak się składa, że ten rzut pokrywa się z przekątną ściany. Dlatego kąt między przekątną sześcianu a ścianą to kąt między przekątną sześcianu a przekątną ściany.

zs6sobieski: zle to jest. powinno byc na odwrot . zaznaczona jest przekatna szescoanu do przekatnej podstawy w tangensie a nie przekatna szescianu do przekatnej sciany bocznej . wtdey α bedzie w kacie u gory i sie zamieni . a sie skroca i zostanie √2

Jakub: Dobrze jest. Ściana boczna jest hmm z boku. To nie jest podstawa.

pablo: a jak bym zostawił samo a/a√2 dostał bym jakieś punkty?

Jakub: Tak. To prawie końcowe rozwiązanie.

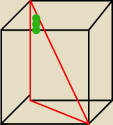
iwona: Te zielone kropki to kąt alfa. Czy to zadanie może być rozwiązane w ten sposób? Wtedy do tangensa podstawiam przyprostokątną naprzeciw alfa, czyli a√2 do przyprostokątnej przy alfie, czyli a, z czego otrzymuję √2.

Jakub: Kąt, który zaznaczyłaś (zielone kropki), to kąt między przekątną sześcianu a krawędzią ściany bocznej, a nie kąt między przekątną a ścianą boczną. Na 966 masz trochę o kątach w sześcianie.

Kuba : jeżeli podałbym wynik, czyli ok 35°, to było by to niezgodne z poleceniem ?

Jakub: W tekście zadania masz "oblicz tangens kąta". Jeżeli podasz kąt, to nie będzie on odpowiedzią do zadania.

Kuba : rozumiem

pawel1984:

	a		1		√2
dlaczego		można zapisać w postaci		x
	a √2		√2		√2

Jakub:

	a
W ułamku		skracam "a", czyli dzielę licznik i mianownik przez "a". Zostaje mi
	a√2

	1		√2
		. Z tego ułamka usuwam niewymierność w mianowniku mnożąc przez		. Zobacz
	√2		√2

przykłady na 1635.