drky: kosinus? nie czasami cosinus? po za tym strona świetna pozdrawiam

Jakub: Można pisać "cosinus" lub "kosinus". To drugie jest bardziej po polsku. Jak masz wyraz "cosinus" to w języku polskim "c" czytasz jak "c" a nie jak "k". Tylko w ten sposób przeczytany "cosinus" brzmi niepoprawnie. Powinno więc się pisać "kosinus". Nie przyjęło się to jednak, z tego co widzę. Tak więc możesz się natknąć i na jedną i na drugą formę. Nawet na mojej stronie piszę różnie, ponieważ nie mogę się zdecydować.

Lenka: Jakub. to jakis mistrzu jest

Kuba92: Pytanie jest chyba źle sformułowane: W zadaniu chodziło o przekątną sześcianu a przekątną podstawy czy o przekątna sześcianu i podstawę?

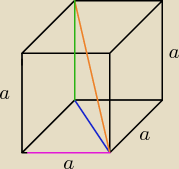
k.c.u: Kuba92 ma racje, bardziej "po polsku" byłoby: Oblicz cosinus kąta między przekątną, a przekątną podstawy sześcianu. Jeszcze nie miałem w ogóle stereometrii ale takie zdanie można też zrozumieć, że sama podstawa czyli różowy odcinek (bok podstawy).

Jakub: Jeżeli jest w zadaniu kąt między przekątną sześcianu a podstawą, to nie można wziąć innego kąta niż między przekątną sześcianu a przekątną podstawy. Po prostu inaczej nie da się zaznaczyć tego kąta. W treści zadania nikt nie będzie szedł ci na rękę i dopowiadał, co to znaczy kąt między przekątną sześcianu a podstawą. To powinieneś wiedzieć ty. Kąt z różowym odcinkiem, o którym piszesz, to kąt między przekątną sześcianu a krawędzią podstawy wychodzącą z tego samego wierzchołka. To jednak co innego. Jak widzisz nie każdy kąt między przekątną sześcianu a jakimś odcinkiem w podstawie to kąt między przekątną sześcianu a podstawą.

k.c.u: A no to już wiem Dziękuje

k.c.u: Dopiero teraz jak czytam na internecie, dowiaduje się wielu ciekawych rzeczy na temat stereometrii Nawet fajny, chodź bardzo podchwytliwy dział

Kwachu: Odpowiedź ^a√6_3a jest poprawna czy nie?

Jakub: Poprawna, chociaż można ją prościej zapisać, czyli skrócić "a".

Adrian: Albo mi się wydaje.... ale przy każdym tego typu zadaniu jest ta samo odpowiedź. podstawiłem sobie: a = 6 d = 6√3 c = 6√2 analogicznie: "a" czyli "6" się skraca i wychodzi nam wynik...ten co w twoim przykładzie. Albo ja robię coś źle, albo faktycznie w każdym sześcianie cosinus jest ten sam A strona bardzo dobra Dzięki niej zdaję sobie na spokojnie cały materiał.

Jakub: Dokładnie. W każdym sześcianie jest taki sam kąt między przekątną a podstawą, czyli zawsze wychodzi ten sam cosinus. Dzięki temu, że liczę na literach uwzględniam wszystkie możliwe długości. Ty np. sprawdziłeś tylko dla jednej a=6.

pawel1984: Witam w końcowym obliczeniu "cosa=apierwiastek z 2 / a pierwiastek z trzech = u√2√3 i tu mam pytanie z kąt się wzieło u√3√3.

Jakub: Usuwam niewymierność z mianownika. W mianowniku jest √3 i jak go pomnożę przez √3 to

	√3
wyjdzie wymierność czyli 3. Mnożę więc cały ułamek przez		, co mogę zrobić, bo
	√3

	√3
		= 1. Przez 1 zawsze mogę mnożyć, bo to nic nie zmienia np. 5*1 = 5
	√3

	√3
Pomnożenie przez		= 1, zmieniło tylko formę (zapis) wyniku. Jego wartość dalej
	√3

jest bez zmian. Usuwanie niewymierności z mianownika jest dobrym zwyczajem, bo się otrzymuje "ładniejsze" wyniki. Nie jest jednak konieczne. Jak zostawisz pierwiastek w mianowniku, to też ci zaliczą. Więcej o usuwaniu niewymierności z mianownika na 1635.

G: Takie zadanie jest możliwe na maturze, lecz mało prawdopodobne Sześcian jak już ma się pojawić to w pytaniu za 1 pkt, ale warto umieć więcej

a: nie bardzo potrafię określać gdzie są "trójkąty,kąty" pomiędzy czymś a czymś, np. między przekątną sześcianu, a krawędzią podstawy " jest na to jakiś sposób? wiem,gdzie trzeba leży krawędź i przekątna, ale skąd wzięć pozostałe informacje?