Ania: dlaczego nie można ze wzoru 1/3h obliczyć promienia?

Ania: już wiem bo to nie jest trójkąt równoboczny

Albert: Dla mnie to i tak za trudne ;x Zawsze mi sie myla sin i cos itd. Bez zagladania do wzorow nie zrobilbym ani jednego zadania.

Jakub: Na maturze masz zestaw wzorów matematycznych, więc możesz zaglądać.

roman: może mi ktoś powiedzieć dlaczego jest tam taki zapis >? chodzi mi dokładnie o ten drugi ułamek

	24√3		6√3
( ... )		=		i pozniej pan usuwania niewymiernosc to
	12+8√3		3+2√3

zawsze trzeba zmieniac znak w mianowniku >? a jesli trzeba to dlaczego >? pozdrawiam

Jakub:

	24√3
Jeśli chodzi o ułamek		to ja go skracam, czyli dzielę wszystko przez 4:
	12+8√3

24√3 : 4 = 6√3 12 : 4 = 3 8√3 : 4 = 2√3 Usuwając niewymierność w mianowniku mnożę przez (3−2√3) ponieważ chcę skorzystać ze wzoru (a+b)(a−b) = a²−b² lub (a−b)(a+b) = a²−b² (mnożenie jest przemienne). Tak więc jak w mianowniku jest suma mnożę przez różnicę, a jak jest różnica mnożę przez sumę. Więcej przykładów na 1635.

Madzia: Jeżeli mamy dodawanie w mianowniku to możemy skracać ?

Jakub: Tak, jeżeli dzielisz każdy składnik dodawania.

Madzia: dzięki

wojtek: moge obliczyc to z pitagorasa? tzn po obliczeniu tego tg30, znam juz dwa wymiary, a jest to trojkat prostokatny o ile sie nie myle?

wojtek: i skad sie wzielo puzniej to 36? przy obliczaniu promienia

Jakub: Tak. Zamiast liczyć cosinus możesz policzyć z twierdzenia Pitagorasa. 6√3 * (3−2√3) = 6√3 * 3 − 6√3 * 2√3 = 18√3 − 12*3 = 18√3 − 36

Lookie: zamotałem się troche bo jak liczyłeś tg 30 stopni to moge tam rownież policzyć zamiast tg ctg30 stopni? wtedy mi wyszlo 6√3 to nie wiem juz kiedys tg a kiedy ctg liczyc eh pomotalo mi się

Lookie: a nie przapraszam poprostu zle odczytalem z tablicy ctg dla 30stopni eh nie było tematu

Lookie: wiec juz sie wyjasnilo ze to nie ma roznicy czy tg czy ctg wezme heh

Kamil: Mnie uczono w gimnazjum, że jak jest 30 stopni przy podstawie to można sobie dorysować drugą część trójkąta równobocznego i też tak zrobiłem. Jest też 120 stopni przy trzecim wierzchołku trójkąta, więc po narysowaniu wysokości jest 60 stopni. Połowa podstawy = 6 i może być ona wysokością trójkąta równobocznego (z dorysowaną częścią). Teraz korzystam ze wzoru na wysokość i wychodzi mi bok trójkąta równoramiennego z zadania, który jest dwa razy większy od jego wysokości więc dziele na pół i h = 2√3, korzystając z tego, że wysokość w okręgu wpisanym jest 1/3h wyszło mi r= 2√3/3. Czy taki wynik tez jest prawidłowy?

Kamil: Już wiem, okrąg nie jest wpisany w trójkąt równoboczny więc nie mogę tak tego zrobić.

Matt: Nie rozumiem. Przecież jest tam trójkąt charakterystyczny, i według tego wysokość wychodzi 6√3. A w zadaniu jest 2√3 w obliczeniu za pomocą tg30.

kaf:

	r
środek okręgu wpisanego leży na przecięciu dwusiecznych kątów. można policzyć tg15=		i z
	6

tego obliczyć r?

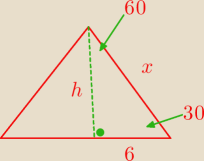
bezendu: po co tg i cos ? wystarczy tylko sin60⁰

	√3
sin600=
	2

√3		6
	=
2		x

√3x=12

	12		√3		12√3
x=		*		=		=4√3
	√3		√3		3

teraz wyliczę h h²=(4√3)²−6² h²=48−36 h²=12 h=2√3 lub h=−2√3∉R₊ więc odrzucam

	1
P=		*2√3*12=12√3
	2

	2*12√3		24√3
r=		=		=12−6√3
	12+8√3		12+8√3

Jakub: Dobre rozwiązanie. Nie sądzę jednak, aby było dużo szybsze od mojego. Ty użyłeś sinusa i Pitagorasa, a ja tangensa i cosinusa. Twoje rozwiązanie jest po prostu trochę inne od mojego.