cierpietnica: Mam prośbę jak rozwiązać takie zadanie:
W ostrosłupie prawidłowym czworokątnym ściany boczne są trójkątami równobocznymi. Oblicz kąt
między sąsiednimi ścianami bocznymi
Nie wiem jak się do tego zabrać

13 mar 18:43
13 mar 19:03
Jakub: | | γ | | √6 | | 2√6 | |
Jak masz sin |
| = |
| , to z tego nie wynika, że sinγ = |
| . Nie ma takiego |
| | 2 | | 3 | | 3 | |
| | γ | | √6 | |
wzoru. Mając sin |
| = |
| trudno wyliczyć sinγ. Lepiej to zrobić |
| | 2 | | 3 | |
z twierdzenia cosinusów (zobacz
543).
(a
√2)
2 = (a
√3/2)
2 + (a
√3/2)
2 − 2*(a
√3/2)*(a
√3/2) * cosγ
| | 3a2 | | 3a2 | | 3a2 | |
2a2 = |
| + |
| − 2 * |
| * cosγ |
| | 4 | | 4 | | 4 | |
| | 6a2 | | 3a2 | |
2a2 = |
| − |
| * cosγ /:a2 |
| | 4 | | 2 | |
To jest już końcowa odpowiedź. Wynik ujemny oznacza, że to jest kąt rozwarty.
13 mar 22:36
xxx: Oblicz pole powierzchni ostrosłupa prawidłowego czworokątnego o krawędzi
bocznej 10 cm wiedząc, że krawędź podstawy ma długość 12 cm.
14 mar 18:13
szalona1810: pomoze ktos?
14 kwi 20:33
Martyna: Musimy wyliczyć wysokość czyli H z Pitagorasa. W podstawie mamy kwadrat czyli czyli 122 daje
nam 144 czyli pole podstawy + pole ściany bocznej czyli 1/2ah czyli 6xto co wychodzi z
Pitagorasa. Pamiętajmy że ściany pocztę są cztery. Wiec pole powierzchni całkowitej to pole
podstawy + 4x pole ściany bocznej. Powodzenia
5 mar 07:46
martaagl26: dana jest siatka ostrosłupa czworokątnego ktoregopodstawa jest kwadrat najdłuzsza krawedz
boczna tego ostrosłupa ma dlugosc pierwiastek z 48 a jego wysokosc jest rowna długosci
podstawy Oblicz objetosc tego ostrosłupa i pole powierzchni całkowitej tego ostrosłupa? ktos
pomoze bo nie mam pojecia jak sie do tego zabrac

3 gru 11:52

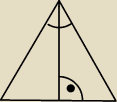 http://img54.imageshack.us/img54/2793/beztytuuwfasx8.png
przyjmując sinγ/2= [1/2a√2 ] / [a√3] /2 = a√2/ a√3 = √6/3
sinγ= 2√6/3
Czy dobrze rozwiązałam?
http://img54.imageshack.us/img54/2793/beztytuuwfasx8.png
przyjmując sinγ/2= [1/2a√2 ] / [a√3] /2 = a√2/ a√3 = √6/3
sinγ= 2√6/3
Czy dobrze rozwiązałam?
