zanetka:)*: nigdy nie umiałam funkcji..ale dzieki tak sie wytłumaczonym zadaniom potrafię to zrobić

16 kwi 13:17
dx626: Przyznam że lepiej wytłumaczone niż w podręcznikach w szkołach średnich
Dzięki
27 maj 22:43
aurade: Dzięki ta strona jest poprostu boska

9 lis 18:12
Kasia: Wielkie dzięki! Jutro z tego sprawdzian

12 gru 15:34
reksio: świetnie wszystko wyjasnione

...
17 lut 10:02
agi: A jakie mają być odpowiedzi do tych zadań?
Poda ktoś bo nie wiem czy dobrze robię?
28 kwi 17:56
28 kwi 17:57
Jakub: Klikaj niebieskie > >, aby zobaczyć rozwiązania zadań.
1 maj 01:59
glonojad: Czy dziedzina są poprostu a oraz b


A:(a,b)→R
20 lip 22:55
Jakub: Do którego zadania odnosi się twoje pytanie?
20 lip 23:31
nick 1: wyznacz dziedzinę funkcji :
f (x)=1/ X⋀2 − 2/x +3
29 lis 19:39
eda: f(x)=
√X+3x
mógłby mi ktoś pomóc?

Trzeba obliczyć dziedzinę i miejsce zerowe
4 sty 20:22
MrG: @eda liczysz normalnie dziedzinę, tak jak masz opisane. A miejsce zerowe to przyrownujesz do 0
i heja

8 sty 18:41
abcd:
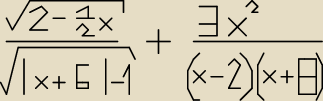
Prosiłbym o trudniejsze zadania, bo z tymi to nie ma problemu

Problem pojawia się wtedy gdy
mam ułamek, pierwiastek i wartość bezwzględną w jednym przykładzie...

Na przykład ten powyżej.
14 lut 18:30
adam: y=log2(x+1) , czy D=(0;+∞)\{1}
i dlaczego, bo mam tak w książce
23 kwi 20:12
Jakub: Nie. Dziedziną y = log2(x+1) jest
x + 1 > 0
x > −1
D = (−1,∞)
23 kwi 22:18
P.: no ja też bym prosiła o trudniejsze przykłady dot. dziedziny np. gdzie trzeba robić wiecej niz
jedno załozenie...
13 lis 19:43
8 sty 22:32
Natt. : dziedziną funkcji f(x)=√x2−2√2+2 jest zbiór:
a) <−√2;√2 b) (−∞−√2 > u < √2 c) R\ { √2 } d) R
8 mar 17:29
Magda: Nie było mnie na lekcji i nie wiem jak to rozwiązać. Mam podać dziedzinę funkcji f(x)
13 mar 19:08
oko555: O kurde
Wielkie dzięki

Ładnie wszystko wytłumaczenie
Jestem pod wrażeniem

25 sie 16:44
Maciek: Jak wyznacza się dziedzinę funkcji f(x)=x2 − 1
29 wrz 18:50
Jakub: Dziedzina f(x) = x
2 − 1 to zbiór wszystkich liczb rzeczywistych, czyli D =
R.
Zobacz
141.
30 wrz 13:55
buuuuuuuuuu: Przydało się

30 wrz 17:37
Michał Mazek: abcd odpowiedź do twojego zadania

: Df= |x+6|−1>0 i (x−2)(x+8)≠0
I. |x+6|−1>0
x+6−1>0
x+5>0
x>−5
II. x−2≠0 i x+8≠0
x≠2 x≠−8
Df=(−5;+
∞)\{2}
miejsc zerowych i zbioru mi się nie chciało

ale przykład ciekawy, dzięki,jutro piszę,
powodzenia.
10 mar 20:10



 ...
...

 A:(a,b)→R
A:(a,b)→R
 Trzeba obliczyć dziedzinę i miejsce zerowe
Trzeba obliczyć dziedzinę i miejsce zerowe

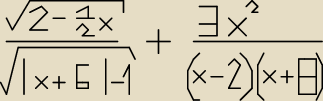 Prosiłbym o trudniejsze zadania, bo z tymi to nie ma problemu
Prosiłbym o trudniejsze zadania, bo z tymi to nie ma problemu  Problem pojawia się wtedy gdy
mam ułamek, pierwiastek i wartość bezwzględną w jednym przykładzie...
Problem pojawia się wtedy gdy
mam ułamek, pierwiastek i wartość bezwzględną w jednym przykładzie...  Na przykład ten powyżej.
Na przykład ten powyżej.
 Ładnie wszystko wytłumaczenie
Jestem pod wrażeniem
Ładnie wszystko wytłumaczenie
Jestem pod wrażeniem 

 : Df= |x+6|−1>0 i (x−2)(x+8)≠0
I. |x+6|−1>0
x+6−1>0
x+5>0
x>−5
II. x−2≠0 i x+8≠0
x≠2 x≠−8
Df=(−5;+∞)\{2}
miejsc zerowych i zbioru mi się nie chciało
: Df= |x+6|−1>0 i (x−2)(x+8)≠0
I. |x+6|−1>0
x+6−1>0
x+5>0
x>−5
II. x−2≠0 i x+8≠0
x≠2 x≠−8
Df=(−5;+∞)\{2}
miejsc zerowych i zbioru mi się nie chciało  ale przykład ciekawy, dzięki,jutro piszę,
powodzenia.
ale przykład ciekawy, dzięki,jutro piszę,
powodzenia.