fen: Robimy tego typu zadania w szkole na poziomie podstawowym.. .

Jakub: Gratulacje dla twojej nauczycielki! Serio.

elika: Czy tego typu zadania z poziomu rozszerzonego mogą się pojawić na podstawowej maturze?

Jakub: Nie. Na podstawie nie są wymagane zadania, które wymagają wzorów kombinatorycznych. Jednak pewnie będzie zadanie, które wymaga znajomości reguły mnożenia. Zobacz 1016. Czasami prościej jest zrobić ze wzorów niż z reguły mnożenia

hmm: w mojej szkole też to wszystko jest na poziomie podstawowym

Jakub: To masz szczęście mieć wysoki poziom w szkole dzięki ambitnym nauczycielom.

Miron: Ja to mam na poziomie rozszerzonym , ale tak nam wytłumaczono wszystko z prawdopodobieństwa , że muszę sie sam uczyć na tej stronie. Dobrze , że taka istnieje

RIsky: Najgorsze jest to, że jak widzę takie zadanie to wydaje mi się, że wiem jak go rozwiązać.... Liczę i wychodzi, jak się okazuje zły wynik, będący w moim przekonaniu dobrym. Niby to rozumiem, a jak przyjdzie do robienia zadań to klapa... eh. P.S. Ale dzięki tej stronie dużo lepiej idzie mi z matematyką. Dzięki.

Pirath: Ja takie zadania rozwiązuję drzewkiem: 1 losowanie: Prawdopodobieństwo, że wylosuję dziewczynę wynosi 12/27 2. losowanie: Prawdopodobieństwo, że wylosuję dziewczynę wynosi 11/26 (1 dziewczyna mniej) Wobec tego prawdopodobieństwo, że wylosuję 2 dziewczyny wynosi 12/27 * 11/26 = 22/117

M: a można to zrobić tak: Ω=27*26=720

	12 1		11 1
A=		*		=132

	22
P(A)=		?
	117

ada: Takie zadania są realizowane na poziomie podstawowym. Ja to mam w podręczniku...a nawet trudniejsze... Nie wiem po co... powinni z nami przećwiczyć jedynie zadania pojawiające się na maturze...

karolina: a ja to bym zrobiła na drzewku i jest o wiele prościej i mniej liczenia pozdrawiam

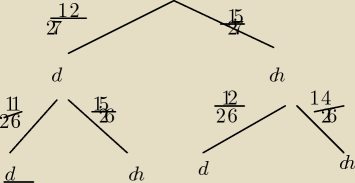
karolina: P(A)=12/27*11/26=66−351=22/117

karolina: maly błąd 66/351=22/117

Gitarzysta93: Ja w tym przypadku skorzystałem ze wzoru na Wariacje bez powtórzeń i po skrócenia ostatecznego wyniku (w którym liczyłem prawdopodobieństwo) dostałem taki sam wynik jak ty Jakubie.Pozdrawiam

Jakub: Też można. Stosując wariacje bez powtórzeń narzucasz ograniczenie, że kolejność losowania jest ważna. Tak więc wylosowanie Kasi i Basi jest czymś innym niż wylosowanie Basi i Kasi. W permutacjach, które ja stosuję, para Kasia i Basia jest tylko jedna, bez względu w jakiej kolejności została wylosowana. Akurat w tym zadaniu nie ma znaczenia, czy narzucasz sobie, że kolejność jest ważna czy nie. I tak dojdziesz do prawidłowego wyniku. Pozdrawiam również.