Gustlik: Wszystko jest w porządku, ale proponowałbym zwrócić przy nierównościach wielomianowych uwagę na jeden bardzo ważny szczegół − ustalenie znaku pierwszego wyrazu wielomianu, jeżeli wielomian podany jest w formie iloczynu wielomianów. Chodzi o to, aby wiadomo było, z której strony patrząc od prawej (z góry czy z dołu) zacząć rysować wykres wielomianu. Ustalić pierwszy wyraz można w następujący sposób: mnożymy przez siebie wszystkie najwyższe potęgi "x" z poszczególnych nawiasów uwzględniając ich współczynniki i znaki, potęgi "x" wraz ze współczynnikami i znakami stojące na początku wielomianu, a w przypadku występowania czynników wielokrotnych (nawias do potęgi) potęgujemy najwyższą potęgę "x" wraz ze współczynnikiem i znakiem z tego nawiasu do potęgi stojącej za nawiasem i następnie mnożymy ten wyraz przez pozostałe najwyższe potęgi "x" w sposób opisany powyżej. W omawianym przykładzie x(x+1)²*(x−2)³>=0 można ustalić pierwszy wyraz następująco: x*x²*x³=x⁶. Skąd wziąłem te czynniki? x występuje na początku wielomianu, x² to najwyższa potęga rozwinięcia czynnika (x+1)², na podobnej zasadzie x³ to najwyższa potęga rozwinięcia czynnika (x−2)³. Pierwszy wyraz jest równy x⁶, ma współczynnik dodatni, a wielomian jest stopnia 6. Wykres rysujemy więc od góry.

Jakub: Masz racje. Ja staram się zapisywać wszystkie wyrażenia w nawiasach w postaci (x−liczba) Dzięki temu liczy się tylko jaka liczba stoi na początku. Dodatnia czy ujemna. Od tego zależy czy zaczynam rysować od góry czy od dołu (oczywiście zaczynam zawsze z prawej strony)

Puzzled: nie rozumiem za bardzo, w takim razie w jakim przypadku rysowaloby sie wykres od dolu? kiedy wszystkie x³ lub x⁵...?

Jakub: Gdy zaczynasz rysować z prawej strony, to liczy się tylko znak na początku wielomianu − przy największej potędze. Jak jest ujemny, to zaczynasz rysować od dołu.

Puzzled: jak to jest w takim razie w przypadku tej nierownosci: (x+3) (x−5)² > 0 ? wdlg reguly, sa dwa pierwiatki −3 i 5 , wykres rysuje sie od gory (bo pierwsze x dodatnie (?)) a ze liczy sie to co jest powyzej osi wiec (−∞,−3) i (5,∞) , tylko ze w odpowidzi jest wynik od (−3,5) i (5,∞).. i tu sie gubie, bo wyglada na to ze prawidlowy wykres w takim razie idzie od dolu.....?

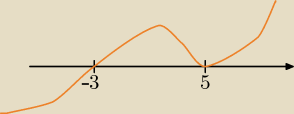
Jakub: (x+3)(x−5)² > 0 Nierówność masz uporządkowaną, czyli w nawiasach najpierw x, a później liczba. Chodzi mi o to, że nie ma np. (3+x) lub (5−x). Teraz wystarczy popatrzyć, co jest na samym początku, a tam jest 1. Nierówność można tak zapisać: 1(x+3)(x−5)² > 0. Liczba 1 jest dodatnia. Pierwiastki wielomianu to x₁ = −3 i x₂ = 5. Pierwiastek x₁ ma krotność nieparzystą, więc wykres przez niego ,,przechodzi''. Pierwiastek x₂ ma krotność parzystą, więc wykres od niego się ,,odbija''. Wygląda mniej więcej tak jak narysowałem. Z niego odczytujesz rozwiązanie nierówności (−3,5)u(5,∞)

Puzzled: ok, dzieki wielkie.. jednego tylko nie rozumiem, dlaczego wykres idzie z dolu a nie z gory. zmienia to zupelnie rozwiazanie tego zadania a przeciez pierwszy x jest dodatni. poza tym gdyby to rownanie mialo postac nastepujaca (−x+3) (x−5)² > 0 to czy wykres "zaczynalby sie" u gory czy ez na dole, oraz czy nadal odbijalby sie przy drugim pierwiastku, przeciez wszystko podniesione do kwadratu daje wartosc dodatnia...?

Jakub: Wykres idzie z góry, ponieważ zaczynam go rysować z prawej strony. Zawsze zaczynam rysować z prawej strony, ponieważ tam są x>0 i można się tylko skupić jaki znak jest na początku wielomianu. Jak dodatni to z góry rysuję, jak ujemny to z dołu. W niektórych szkołach uczą jak rysować od lewej strony, ale wtedy jest dużo trudniej określić, czy od dołu, czy od góry się zaczyna. Trzy różne wersje tego równania dla rozjaśnienia. 1. (−x+3)(x−5)² > 0 −(x−3)(x−5)² > 0 x₁ = 2, x₂ = 5 zaczynam rysować od dołu, w 5 odbijam, w 3 przecinam 2. (x−3)(−x−5)² > 0 (x−3)[−(x+5)]² > 0 (x−3)(x+5)² > 0 x₁ = 3, x₂ = −5 zaczynam rysować od góry, w −5 odbijam, w 3 przecinam 3. (3−x)(5+x)² > 0 (−x+3)(x+5)² > 0 [−(x−3)](x+5)² > 0 −(x−3)(x+5)² > 0 x₁ = 3, x₂ = −5 zaczynam rysować od dołu, w −5 odbijam, w 3 przecinam Jak widzisz, zawsze przekształcam to co jest w nawiasach do postaci x plus/minus liczba.

Puzzled: ok, juz rozumiem w czym rzecz. dziekuje za wyjasnienie

Edzia: napisales ze krotnosc liczby 5 jest przysta a 5*5 =25 wiec nieparzysta wiec nierozumiem czym jest krotnosc

Jakub: Krotność biorę z wykładnika potęgi, z której otrzymuję pierwiastek. W tym wypadku pierwiastek −1 wziąłem z (x+1)². Wykładnik tej potęgi jest równy 2, więc taka jest krotność pierwiastka −1.