imię lub nick :P: troche to wszystko na tej stronie pokrecone... trzeba skakac od odnosnika do odnosnika potem
wracac.... troche to malo praktyczne... ale ogolnie dobrze za ktos pomyslal zeby zrobic taka
stronke zawsze sie przyda jesli ktos czegos nie rozumie.
24 lut 15:50
sandra: dzięki tej stronce pisze teraz lepiej sprawdziany

2 mar 16:29
Kis: rewelacja, teraz na pewno zdam mature!

16 mar 16:02
Karol: Bardzo dobra stronka.
wszystko ładnie pięknie objaśnione.
Wielki plus dla tego co tą stronkę założył
21 kwi 21:14
Myrthan: No dokładnie siedze tutaj pare dni bodajże a już opanowałem cały dział wielomianów sam : D
Robiłem zdanka ze zbioru kiełbasy i idzie jak spłatka. Teraz funkcja wymierna
4 maj 19:26
moni: to jest swietna stronka

może zdam mature... hehe
26 maj 12:14
Tomek: Aham, przydaje się bardzo, polecam robić zadania z kiełbasy

Fajne są
1 cze 21:03
pit: nie rozumiem wzsystkiego
16 sie 18:24
Jakub: Napisz, czego nie rozumiesz.
16 sie 21:18
Mira: Jesteś mistrzem, normalnie kocham tę stronkę

Dzięki niej zdałam z matmy w tamtym roku szkolnym. Jutro mam kartkówkę, więc się uczę.
Załapałam już połowę materiału.
Dzięki wielkie!

21 wrz 19:50
ania: co jeżeli w podstawie mamy samo x? jaka wtedy będzie dziedzina funkcji wymiernej, D=R−{0} ?
albo to samo pytanie tylko z x do kwadratu ? wiem, ze banał ale nie mogę nigdzie tego w
zeszycie znaleźć :C
Ps. świetna stronka, kiedy czegoś w szkole nie załapie to tutaj zawsze jest to dobrze
wyjaśnione.
26 wrz 12:53
Jakub: Dokładnie ania. Jak masz w mianowniku samo x, to dziedziną jest D=R\{0}. Tak samo
jest, jak masz x2.
3 paź 21:02
Marcelina;)): bogu dzięki za takie strony

!
z matematyki jestem kompletna dętka, ale tutaj wszystko można zrozumieć krok po kroku

DZIEKI O WIELKI MATEMATYKU

!

20 paź 17:56
bry: a nie ma żadnych zastrzeżeń do dziedziny ?
31 paź 20:18
roman: PRZEPRASZAM WSZYSTKICH ALE CZY MOZE MI KTOS WYTŁUMACZYC JEDNO ... WŁASCIWIE DWA PRZYKLADY >?
W JEDNYM Z PIERWSZYCH ZADAN JEST WYNIK −3/2 I JEST NAPISANE ZE D= R\{−3/2 }
NATOMIST W INNYM PRZYKLADZIE JEST WYNIK −4/3 I ODP. BRZMI ZE NIE MA TAKICH LICZB RZECZYWISTYCH
SPELNIAJACH TAKIE ROWNANIE ...
I NIE WIEM DLACZEGO RAZ JEST TAK A RAZ INACZEJ ....
dziękuję za odopowiedzi ...
pozdrawiam

30 gru 14:56
nie: ponieważ x
2 zawsze będzie na plusie

−2
2=4
2
2=4
25 sty 21:36
Jakub: @roman
Szukam liczb, które wstawione za x dają zero w mianowniku. Jak wiadomo mianownik ułamka nie
może się równać zero (nie wolno dzielić przez zero).
1) Równanie 2x+3=0 udało się rozwiązać, więc −32 wyrzucam z dziedziny.
2) Równanie 3x2+4=0 nie ma rozwiązania, więc nie mam czego wyrzucić z dziedziny.
25 sty 22:04
maciek: czyli rozumiem to jest dla tego że x2 = −43 po prostu nie mozna go spierwiastkowac tzn
jest nie do rozwiazania i w ten sposob nie mozna go wyrzucic z dziedziny
30 sty 15:35
Jakub: Zgadza się. Nie można spierwiastkować liczby ujemnej −43, więc nie ma wyników. Nie ma
czego wyrzucać z dziedziny.
30 sty 15:37
Piotr: (x+1)(x+2)/(x+1) ,jaka jest dziedzina Dzięki za podpowiedź
23 lut 03:48
Piotr: R czy R/{−1}
23 lut 03:49
Jakub: | | (x+1)(x+2) | |
Dziedzina wyrażenia |
| to R\ {−1} |
| | x+1 | |
23 lut 16:52
MaciejeQ: a czy przy określaniu dziedziny z wyrażenia (x
2 + 1) mamy koniunkcję 1 i −1 czy alternatywę?
Chodzi mi o te śmieszne znaczki ( v )

14 mar 19:51
Jakub: Jak rozumiem, to x2+1 jest w mianowniku. Tak?
Wyrażenie x2+1 jest zawsze dodatnie, więc dziedzina to cały zbiór liczb rzeczywistych.
14 mar 20:08
Lena: a ja mam takie pytanie. Można spierwiastkować 1? Bo jeżeli nie można pierwiastkować −4/3 to
czemu można 1? a 2 można? Bo jest tak: x
2=1 x=−1 x=1
Gdyby było x
2=2 to byłoby x=−2 x=2 ? A może nie można pierwiastkować
tylko ułamków? Proszę o odpowiedź

3 kwi 20:11
Jakub: Nie chodzi o ułamki tylko o minus. Jak masz równanie x2=1, to sobie zadajesz pytanie, co
podniesione do kwadratu daje 1. Odpowiedzią są dwie liczby −1 i 1. W przypadku np. x2=−4 nie
ma dobrej odpowiedzi, ponieważ cokolwiek podnosisz do kwadratu wychodzi wynik dodatni, a nie
ujemny −4. Podobnie jest z −43
4 kwi 00:07
Lena: uhm. No dziękuję, już rozumiem.
4 kwi 10:20
Ania: x2−2x
________
x3
7 kwi 19:45
Jou: (x−2)2*(x+2)=0, dziedzina D= R\{−2,2}, tu mnie cos zastanawia bo ja bym zrobił to tak
(x−√2)*(x+√2)*(x+2)=0, i dziedzina jest równa D=R\{− √2,√2,−2}
20 kwi 13:23
Jakub: (x−√2)*(x+√2) = x2 − (√2)2 = x2−2 To jest jednak co innego niż (x−2)2.
21 kwi 00:11
Jou: a widzisz ja zawsze cos przekombinuje dzieki

21 kwi 15:26
Mikołaj: 4x3− 8x2−x+2 , może ktoś wytłumaczyć?
22 maj 15:00
jkhgkdsz: chujowa strona
27 maj 08:40
Aga: Jak to zrobić? Wyznacz dziedzinę funkcji wymiernej, jesli:
F(X)=x3+x+7/x4+x2−20
F(x)= x+2/4x3−8x2−x+2
F(x)=x−3/5x3−15x2−5x+15
28 maj 11:33
urke: jak wyznaczyc dzidzinę jeśli mamy normalne wyrazenie? z dodawaniem lub odejmowaniem?
np x2−3x (licznik) 2x+1 (mianownik) +10x2+5x (l) x4−5x3 (m) ?
6 cze 15:36
9 sie 08:24
Piotrek: Jest literówka w czwartym czy piątym przykładzie "dziedzina tego wyrażenia wymiernego to
wszystkich liczby rzeczywiste"

11 wrz 20:52
Jakub: Poprawiłem, dzięki.
12 wrz 00:02
kolo: a w takich przykładach jaka będzie dziedzina a) 4x+3y / 9y
4−16x
2 
?
b) 2x+3y / y
2−9−x
2+6x
5 paź 21:06
wawrzek: jakubie możesz mi pomóc

nie rozumiem przedostatniego przykładu.
23 sty 13:34
Jakub: A co w nim nie rozumiesz?
23 sty 18:37
Monnina: Witam.
> a jeśli wychodzi z obliczenia delty 0, w taki razie obliczamy jedno miejsce zerowe i
dziedziną funkcji beda liczby rzeczywiste oprócz właśnie cyfry z tego wyniku.
x2 − 6x + 9 w mianowniku.
wychodzi = 0
zatem jedno miejsce zerowe = 3
Czy nie pomieszałam tego za bardzo
19 lut 00:46
blebleble: mam problem z rozwiązaniem takiego oto zadania będę wdzięczna za pomoć

Treść zadania:
| | x | |
Jeżeli x ≠ −1, to wrażenie |
| −1 jest równe |
| | x+1 | |
6 mar 13:54
prosto: Panie Jakubie, wiem ze pytanie banalnie proste ale treści następującej. Otóż z jakiego powodu
x2=1 lub x2= −1 a x3=1 bez lub. Pytanie napewno bardzo łatwe dla Pana, dla mnie zaś nie
zrozumiałe. Pozdrawiam serdecznie. Gratuluje stronki
6 mar 19:41
Jakub: Jak masz x2 = 1, to są dwa rozwiązania x = −1 lub x = 1.
Jak masz x3 = 1, to jest jedno rozwiązanie x = 1. Dlaczego tylko jedno? Spróbowałem podstawić
−1 i nie wyszło 1 (prawa strona równania). (−1)3 = (−1) * (−1) * (−1) = −1.
6 mar 21:40
Łukasz: Nie wiem w jaki sposób z:
x2(x−2)−4(x−2) = 0
zrobiło się:
(x−2)(x2−4)=0
a następnie:
(x−2)(x−2)(x+4) = 0
?
18 mar 18:02
Emka: Strona super!

18 kwi 21:22
Fan: Uwielbiam Cię Jakubie za tą stronę!
19 kwi 21:46
Marlena: Chciałabym się dowiedzieć, czy zawsze przed rozwiązywaniem takich zadań trzeba liczyć
dziedzinę?
5 maj 16:45
Jakub: Hmm. W poleceniu tego zadania jest, aby policzyć dziedzinę.
5 maj 17:41
Marlena: Chodzi mi o rozwiązywanie wyrażeń wymiernych.
Fakt, mogłam to lepiej ująć

5 maj 21:53
Jakub: W zadaniach z wyrażeniami wymiernymi najczęściej trzeba policzyć dziedzinę. Chodzi o to, że
często się zdarza, że rozwiązując równanie (nierówność) wymierną wychodzi jakiś wynik, który
jednak nie jest prawidłowy, ponieważ nie należy do dziedziny (daje zero w mianowniku). Taki
wynik trzeba odrzucić, ale najpierw trzeba mieć dziedzinę, aby stwierdzić, że dana liczba do
niej nie należy.
5 maj 22:15
Marlena: Będę pamiętać. Dziękuję

6 maj 14:53
Marcin: Jak to obliczyć proszę wyjaśnijcie. 17x3−13x+2x2−5x+6
18 cze 21:32
nieważne: może zdam mature ale chyba raczej niestety w sierpniu

18 lut 15:01
Weronika: Łukasz: Nie wiem w jaki sposób z:
x2(x−2)−4(x−2) = 0
zrobiło się:
(x−2)(x2−4)=0
a następnie:
(x−2)(x−2)(x+4) = 0
?
podbijam pytanie, sama też nie za bardzo rozumiem o co w tym chodzi.
18 lut 18:10
domsi: jak określić dziedzine w tym wyrażeniu: 2x−2/x2 +2 ?
28 lut 19:40
Dominika: | | 2x−2 | |
jak okreslić dziedzine w wyrażeniu |
| ? |
| | x2+x | |
28 lut 19:43
Bóła :): Panie Jakubie: jak mamy x
2−1=0, to zawszę się pytam: co do kwadratu daje JEDEN. no oczywiście,
| | 4x2 | |
−1, 1; ale jeszcze w tym przykładzie: |
| ; no to dziedzina to będzie 1, −1; a czemu |
| | x2−1 | |
nie ma
√1 i −
√1?
27 kwi 18:19
Jakub: Przecież √1 = 1 i −√1 = −1.
28 kwi 15:20
Bóła :): mea culpa

Panie Jakubie za dużo sie uczyłem, dziś znów 8H, maratonik, pod koniec, liczyłem
na kalkulatorze 2 * 1 = bo byłem pewien, że to jeden

. Nie wiem, czy oglądał Pan film
(odbiegając od tematu) "Rok 1984", tam również wmawiano jednemu z głównych bohaterów, że
2*2=5, czasem 3, a czasem każdy z możliwych wyników

. Ja dziś to samo miałem

. Dziękuje za
odpowiedź

.
28 kwi 21:24
Jakub: Filmu nie oglądałem, ale czytałem książkę

Znaczy słuchałem, bo to był audiobook. Na
szczęście matematyka jest niezależna od polityki władzy. Nie da się wmówić, czegoś co jest
nielogiczne.
29 kwi 00:13
Grzesiek: W przykładzie z − 4/3 jest błąd: w odpowiedzi jest napisane, że "nie ma liczb rzeczywistych
spełniających równanie" dlatego D=R.
1 cze 15:33
TheLawPL: Przydałoby się uzupełnienie o przykłady z wartościami bezwzględnym dla tych, co mają
rozszerzoną, a to co teraz jest, wystarczająco tłumaczy podstawowe przykłady.
9 paź 19:45
Jakub: @Grzesiek
To nie jest błąd. Nie ma liczby, którą podniesiona do kwadratu daje liczbę ujemną −43,
dlatego do dziedziny należą wszystkie liczby rzeczywiste.
20 kwi 18:27
Tolaa: Hej

mam problem z dwoma założeniami :
a) 6x
2 − 2
b)1000x
2+1
Proszę o pomoc

pilne!
3 wrz 17:12
Paula:
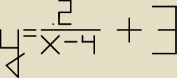
Jak określić dziedzinę funkcji
12 mar 18:29


 może zdam mature... hehe
może zdam mature... hehe
 Fajne są
Fajne są
 Dzięki niej zdałam z matmy w tamtym roku szkolnym. Jutro mam kartkówkę, więc się uczę.
Załapałam już połowę materiału.
Dzięki wielkie!
Dzięki niej zdałam z matmy w tamtym roku szkolnym. Jutro mam kartkówkę, więc się uczę.
Załapałam już połowę materiału.
Dzięki wielkie! 
 !
z matematyki jestem kompletna dętka, ale tutaj wszystko można zrozumieć krok po kroku
!
z matematyki jestem kompletna dętka, ale tutaj wszystko można zrozumieć krok po kroku DZIEKI O WIELKI MATEMATYKU
DZIEKI O WIELKI MATEMATYKU !
!


 −22=4
22=4
−22=4
22=4







 ?
b) 2x+3y / y2−9−x2+6x
?
b) 2x+3y / y2−9−x2+6x
 nie rozumiem przedostatniego przykładu.
nie rozumiem przedostatniego przykładu.
 Treść zadania:
Treść zadania:




 Panie Jakubie za dużo sie uczyłem, dziś znów 8H, maratonik, pod koniec, liczyłem
na kalkulatorze 2 * 1 = bo byłem pewien, że to jeden
Panie Jakubie za dużo sie uczyłem, dziś znów 8H, maratonik, pod koniec, liczyłem
na kalkulatorze 2 * 1 = bo byłem pewien, że to jeden  . Nie wiem, czy oglądał Pan film
(odbiegając od tematu) "Rok 1984", tam również wmawiano jednemu z głównych bohaterów, że
2*2=5, czasem 3, a czasem każdy z możliwych wyników
. Nie wiem, czy oglądał Pan film
(odbiegając od tematu) "Rok 1984", tam również wmawiano jednemu z głównych bohaterów, że
2*2=5, czasem 3, a czasem każdy z możliwych wyników  . Ja dziś to samo miałem
. Ja dziś to samo miałem  . Dziękuje za
odpowiedź
. Dziękuje za
odpowiedź  .
.
 Znaczy słuchałem, bo to był audiobook. Na
szczęście matematyka jest niezależna od polityki władzy. Nie da się wmówić, czegoś co jest
nielogiczne.
Znaczy słuchałem, bo to był audiobook. Na
szczęście matematyka jest niezależna od polityki władzy. Nie da się wmówić, czegoś co jest
nielogiczne.
 mam problem z dwoma założeniami :
a) 6x2 − 2
b)1000x2+1
Proszę o pomoc
mam problem z dwoma założeniami :
a) 6x2 − 2
b)1000x2+1
Proszę o pomoc  pilne!
pilne!
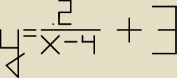 Jak określić dziedzinę funkcji
Jak określić dziedzinę funkcji