Antonina 66: Proszę Jakubie o wytłumaczenie w punktach abym lepiej to zrozumiała
,bo egzamin tuz,tuz.
Najlepiej krok po kroku Będzie mi łatwiej
Za co serdeczne dzięki.
Stronka bardzo pomocna do samodzielnej nauki ale niekiedy jest niezbędna pomoc nauczycieli.
Myślę o Was ,Drodzy
13 maj 13:39
Jakub: Napisz mi, którego przykładu z poprzedniej strony nie rozumiesz. Ciężko mi wszystko opisać.
13 maj 21:23
wqable: jak sie niweluje nawiasy w wielomianach to nalezy zmienic znak, tak? to by wyjasnilo dlatego
tak zrobiles w odejmowaniu...
20 maj 16:39
Jakub: Znak przed nawiasem dotyczy wszystkich potęg w środku. Plus nic nie zmienia natomiast jak jest
przed nawiasem minus, to opuszczając nawias zmieniamy znak przy każdej potędze.
20 maj 18:45
NOVY: czemu w pierwszym przykładzie W(x) + P(x)= (2x5
3−2x
2 i tak dalej potem z
tego wszystkiego = 2x
3 −x
2 −2x−4 czyli z tego nawiasu (−x
2−3x) wynika że
wypisałeś tylko te −x
2 czemu tylko to jedno? w innych przykładach gdzie jest np.
odejmowanie odejmujesz cały nawias a tu tylko te −x
2 , please napisz czemu ..

18 lip 14:54
Jakub: Rozpiszę to dokładniej, chociaż w szkolnych obliczeniach, aż tak dokładnie się nie pisze:
W(x)+P(x) = ( 2x3 − 2x2 + x − 4 ) + ( x2 − 3x ) =
= 2x3 − 2x2 + x2 + x − 3x − 4 =
= 2x3 − x2 − 2x − 4
19 lip 17:36
NOVY: no, teraz już jasne

, dzięki za wysiłek.
19 lip 18:47
Pat: Dzięki wielkie, przydało mi się.
29 wrz 00:07
Adam: Witam jak rozłożyc wielomian x3− x2−17x−15 na iloczyn (x− 5)(x+3)(x+1), jest to przykład ze
strony "Rozkład wielomianu na czynniki". Czy możesz przedstawić to krok po kroku?
Pozdrawiam
15 lis 19:18
czeski: Ponieważ, drogi Adamie, jest to wielomian trzeciego stopnia, więc ma on trzy pierwiastki,
którymi są 5, (−3) oraz (−1). Korzystając z postaci iloczynowej tak to właśnie wygląda.
14 sty 01:47
Zuzka: W końcu coś,co sama zrobiłam

I co najważniejsze−zrobiłam dobrze!
Tak to jest jak się zaczęło szkołę po "nastu" latach przerwy.A takich rzeczy jak te tutaj,to ja
nawet wcześniej na oczy nie widziałam.
Tym bardziej jestem dumna z siebie.
Ale to wszystko dzięki P.Jakubowi

.Śledzę wszystkie stronki i staram się ogarniać materiał.
18 lut 19:18
adamski: W (X) =x2−1
p(x)2x2+4x+1
wyznacz wielomian w(x)2[w(x)]2−p(x)
z góry dziękuje
1 mar 12:10
aaaa: Co zrobic jezeli wielomina mamy pomnozyc badz dodac, a jest on w nawiasie i podciagniety do
2

Prosze o odpowiedz bo poleglem przy jednym zadaniu na sprawdzianie
19 mar 10:13
Jakub: Trzeba podnieść ten wielomian do kwadratu. Na przykładzie wygląda to tak:
(x3−x+1)2 =
= (x3−x+1) * (x3−x+1) = (mnożę "każdy przez każdy")
= x6 − x4 + x3 − x4 + x2 − x + x3 − x + 1 =
= x6 − 2x4 + 2x3 + x2 − 2x + 1
19 mar 13:36
..klaud..: skroc wyrazenie wymierne . Napisz potrzebne zalozenia :
8x(do 3 potegi) + 1 / 2x + 1
22 mar 19:28
albi: 3p(2) * 3p(2)
10 cze 19:23
albi: prosze o pomoc : (3 pierwiastki z dwoch + 2) razy (3 pierwiastki z dwoch minus dwa) Bardzo
prosze o jak najszybszą pomoc

!
10 cze 19:25
Jakub: Od tego są komentarze, abyś pytał się, jak czegoś nie wiesz.
22 wrz 23:43
Arven: (x3−x+1)2 = (x3−x+1) * (x3−x+1) =
= x6 − x4 + x3 − x4 + x2 − x + x3 − x + 1 =
= x6 − 2x4 + 2x3 + x2 −2x + 1
↖Tu ma być 2x nie −x bo wyżej są dwa ixy a −x+(−x)= 2x
23 paź 12:03
monii: Arven, tam jest dobrze
− x + ( − X )= to jest tak samo jak − x − x=2x
19 lis 11:07
Jakub: Arven dobrze napisał −x−x = −2x. Dzięki, poprawiłem.
19 lis 15:47
mili: rozumiem jak sie rozpisuje przykład że przepisuje sie od najwyzszej potęgi aż do liczby bez X
ale nie rozumiem skąd sie wział wynik np. 2x2 − x2 − 2x − 4
Proszę o pomoc
20 gru 21:23
Jakub: 2x3 przepisałem, −3x2 otrzymałem z −2x2−x2, 4x otrzymałem z x+3x, −4 przepisałem.
Po prostu dodaję potęgi o tych samych wykładnikach.
20 gru 23:02
Ania: Znajdź iloczyn liczb będących rozwiązaniami równania : (x2−1)(x3+1)=0 .
Proszę o pomoc.
Pozdrawiam.
9 sty 18:44
Gientus: Jakub dużo robisz, lecz na stronce nie idzie się nic nauczyć ..

przydaje się tylko do
ćwiczenia na przykładach ... ( Tylko po to żeby nie musieć samemu żadnych wymyślać )
26 mar 16:45
Gustlik:
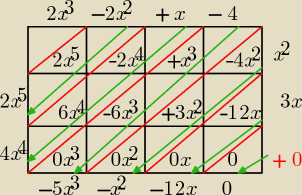
Nowy ciekawy sposób mnożenia wielomianów:
(2x
3−2x
2+x−4)(x
2+3x)=2x
5+4x
4−5x
3−x
2−12x
Sposób ten opracowałem na podstawie nowego sposobu mnożenia liczb przedstawionego na stronie:
https://matematykaszkolna.pl/forum/forum.py?komentarzdo=141 .
Podobnie jak dla mnożenia liczb rysujemy tabelkę o rozmiarach zależnych od ilości wyrazów obu
wielomianów. Tutaj mamy wielomian 4−wyrazowy i 3−wyrazowy.
UWAGA  !
! W przypadku niepełnych wielomianów, czyli takich z "brakującymi" wyrazami te
"brakujące" wyrazy wpisujemy ze współczynnikiem
0 i do tego odpowiednia potęga x i
traktujemy ten wyraz jak każdą inną liczbę. W tym przykładzie takim niepełnym wielomianem jest
ten drugi − "brakuje" wyrazu wolnego.
Mnożymy poszczególne wyrazy pierwszego wielomianu przez wyrazy drugiego [P[uwzględniając
oczywiście znaki]] i wynik mnożenia wpisujemy w odpowiednie pole na przecięciu odpowiedniego
wiersza z odpowiednią kolumną w odróżnieniu od liczb
zawsze pod przekątną, nawet jeżeli
wynikowy współczynnik jest dwu− i więcej cyfrowy. Liczby dwucyfrowe wpisywaliśmy wg zasady:
dziesiątki nad przekatną, a jedności pod przekątną. Tutaj cały wyraz
pod przekątną, aby
cyfry nie mieszały się z innymi potęgami x. Nastepnie podobnie jak z liczbami sumujemy wyrazy
po przekątnych, jak pokazują
zielone strzałki i otrzymane wyrazy wpisujemy z boku lub pod
tabelką na wysokości odpowiedniej przekątnej i mamy wielomian wynikowy. Należy zauważyć, że w
każdej przekątnej bedziemy mieli wyrazy podobne, tj. z tą samą potęgą x, które można sumować
(redukować). Nie musimy wyszukiwać tych wyrazów, jak to ma miejsce w klasycznej metodzie, bo
one same się ładnie "ułożą" po przekątnych. Sposób moim zdaniem ciekawy i bardziej
przejrzysty, zwłaszcza przy mnożeniu wielomianów dużych stopni, bo są one "długie" i
tradycyjnym sposobem można łatwo się pomylić, np. zgubić wyraz albo znak.
19 kwi 02:05
NowyGoras: Mam mały problem z doprowadzeniem ułamka do najprostszej postaci.
Jak uprościć ten ułamek żeby otrzymać wynik x+1?
2 maj 17:37
Jakub: Pomnóż licznik i mianownik przez x, a następnie rozbij wielomian w liczniku ze wzoru skróconego
mnożenia (strona
55) a
3 + b
3 = (a+b)(a
2−ab+b
2)
2 maj 21:50
NowyGoras: @Jakub dziękuję. Teraz stało się wszystko jasne.
3 maj 12:04
Mela: nie do końca rozumiem jak rozwiązać z tego 1 przykładu 3 przykład! Jakubie czy mógłbyś wypisać
w punktach jak to zrobić
8 paź 12:45

 , dzięki za wysiłek.
, dzięki za wysiłek.
 I co najważniejsze−zrobiłam dobrze!
Tak to jest jak się zaczęło szkołę po "nastu" latach przerwy.A takich rzeczy jak te tutaj,to ja
nawet wcześniej na oczy nie widziałam.
Tym bardziej jestem dumna z siebie.
Ale to wszystko dzięki P.Jakubowi
I co najważniejsze−zrobiłam dobrze!
Tak to jest jak się zaczęło szkołę po "nastu" latach przerwy.A takich rzeczy jak te tutaj,to ja
nawet wcześniej na oczy nie widziałam.
Tym bardziej jestem dumna z siebie.
Ale to wszystko dzięki P.Jakubowi .Śledzę wszystkie stronki i staram się ogarniać materiał.
.Śledzę wszystkie stronki i staram się ogarniać materiał.
 Prosze o odpowiedz bo poleglem przy jednym zadaniu na sprawdzianie
Prosze o odpowiedz bo poleglem przy jednym zadaniu na sprawdzianie
 !
!
 przydaje się tylko do
ćwiczenia na przykładach ... ( Tylko po to żeby nie musieć samemu żadnych wymyślać )
przydaje się tylko do
ćwiczenia na przykładach ... ( Tylko po to żeby nie musieć samemu żadnych wymyślać )
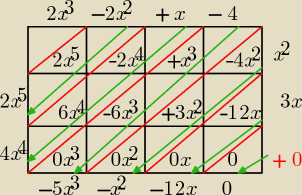 Nowy ciekawy sposób mnożenia wielomianów:
(2x3−2x2+x−4)(x2+3x)=2x5+4x4−5x3−x2−12x
Sposób ten opracowałem na podstawie nowego sposobu mnożenia liczb przedstawionego na stronie:
https://matematykaszkolna.pl/forum/forum.py?komentarzdo=141 .
Podobnie jak dla mnożenia liczb rysujemy tabelkę o rozmiarach zależnych od ilości wyrazów obu
wielomianów. Tutaj mamy wielomian 4−wyrazowy i 3−wyrazowy.
UWAGA
Nowy ciekawy sposób mnożenia wielomianów:
(2x3−2x2+x−4)(x2+3x)=2x5+4x4−5x3−x2−12x
Sposób ten opracowałem na podstawie nowego sposobu mnożenia liczb przedstawionego na stronie:
https://matematykaszkolna.pl/forum/forum.py?komentarzdo=141 .
Podobnie jak dla mnożenia liczb rysujemy tabelkę o rozmiarach zależnych od ilości wyrazów obu
wielomianów. Tutaj mamy wielomian 4−wyrazowy i 3−wyrazowy.
UWAGA  ! W przypadku niepełnych wielomianów, czyli takich z "brakującymi" wyrazami te
"brakujące" wyrazy wpisujemy ze współczynnikiem 0 i do tego odpowiednia potęga x i
traktujemy ten wyraz jak każdą inną liczbę. W tym przykładzie takim niepełnym wielomianem jest
ten drugi − "brakuje" wyrazu wolnego.
Mnożymy poszczególne wyrazy pierwszego wielomianu przez wyrazy drugiego [P[uwzględniając
oczywiście znaki]] i wynik mnożenia wpisujemy w odpowiednie pole na przecięciu odpowiedniego
wiersza z odpowiednią kolumną w odróżnieniu od liczb zawsze pod przekątną, nawet jeżeli
wynikowy współczynnik jest dwu− i więcej cyfrowy. Liczby dwucyfrowe wpisywaliśmy wg zasady:
dziesiątki nad przekatną, a jedności pod przekątną. Tutaj cały wyraz pod przekątną, aby
cyfry nie mieszały się z innymi potęgami x. Nastepnie podobnie jak z liczbami sumujemy wyrazy
po przekątnych, jak pokazują zielone strzałki i otrzymane wyrazy wpisujemy z boku lub pod
tabelką na wysokości odpowiedniej przekątnej i mamy wielomian wynikowy. Należy zauważyć, że w
każdej przekątnej bedziemy mieli wyrazy podobne, tj. z tą samą potęgą x, które można sumować
(redukować). Nie musimy wyszukiwać tych wyrazów, jak to ma miejsce w klasycznej metodzie, bo
one same się ładnie "ułożą" po przekątnych. Sposób moim zdaniem ciekawy i bardziej
przejrzysty, zwłaszcza przy mnożeniu wielomianów dużych stopni, bo są one "długie" i
tradycyjnym sposobem można łatwo się pomylić, np. zgubić wyraz albo znak.
! W przypadku niepełnych wielomianów, czyli takich z "brakującymi" wyrazami te
"brakujące" wyrazy wpisujemy ze współczynnikiem 0 i do tego odpowiednia potęga x i
traktujemy ten wyraz jak każdą inną liczbę. W tym przykładzie takim niepełnym wielomianem jest
ten drugi − "brakuje" wyrazu wolnego.
Mnożymy poszczególne wyrazy pierwszego wielomianu przez wyrazy drugiego [P[uwzględniając
oczywiście znaki]] i wynik mnożenia wpisujemy w odpowiednie pole na przecięciu odpowiedniego
wiersza z odpowiednią kolumną w odróżnieniu od liczb zawsze pod przekątną, nawet jeżeli
wynikowy współczynnik jest dwu− i więcej cyfrowy. Liczby dwucyfrowe wpisywaliśmy wg zasady:
dziesiątki nad przekatną, a jedności pod przekątną. Tutaj cały wyraz pod przekątną, aby
cyfry nie mieszały się z innymi potęgami x. Nastepnie podobnie jak z liczbami sumujemy wyrazy
po przekątnych, jak pokazują zielone strzałki i otrzymane wyrazy wpisujemy z boku lub pod
tabelką na wysokości odpowiedniej przekątnej i mamy wielomian wynikowy. Należy zauważyć, że w
każdej przekątnej bedziemy mieli wyrazy podobne, tj. z tą samą potęgą x, które można sumować
(redukować). Nie musimy wyszukiwać tych wyrazów, jak to ma miejsce w klasycznej metodzie, bo
one same się ładnie "ułożą" po przekątnych. Sposób moim zdaniem ciekawy i bardziej
przejrzysty, zwłaszcza przy mnożeniu wielomianów dużych stopni, bo są one "długie" i
tradycyjnym sposobem można łatwo się pomylić, np. zgubić wyraz albo znak.