kkkk: nie rozumiem. dlaczego −1?

Jakub: Kliknij niebieski link na poprzedniej stronie: "Odległość liczb na osi liczbowej".

lusia: mi to nic nie mowi

kazik: ja tez nie rozumiem dlaczego −1

Jakub: |x+1| = 3 |x−(−1)| = 3 Zamieniłem x+1 na x−(−1), ponieważ w takiej postaci widać, że szukam liczb odległych od −1 o 3. W wartości bezwzględnej musi być odejmowanie, jak mam skorzystać z wiadomości na stronie 1093.

Karol: panie jakubie dalej nie rozumiem dlaczego −1 mógłby pan prościej?

Justyna: ja to tak rozumiem: |x+1|=3 trzeba zgadnąć x, aby to zrobić należy sie zastanowić jaką liczbe wynosi x tak aby równianie w patyczkach (|x+1|) wynosiło 0 i tu pasuje tylko −1, bo −1+1=0

Jakub: Też dobry sposób Justyna. Tylko, że tu jest narzucony w treści zadnia sposób rozwiązywania.

Zuzka: Ja,żeby obliczyć −1,wyznaczam miejsce 0 (zerowe) Ix+1I=3 x+1=0 x=−1 1 jest przenoszone na drugą stronę znaku=więc zmieniamy znak. Tak nam babka na zajęciach tłumaczyła i w ten sposób najłatwiej to wychodzi. Potem wystarczy obliczyć 3 "kroki"od −1 w prawo i 3 w lewo na osi.Wynik łatwo odczytać.

Jakub: Też dobry sposób Zuzka

Kondzio: Ja mam inną meodę { x + 1 } = 3 x + 1 = 3 i x + 1 = −3 x = 2 x = −4

Jakub: Dobry sposób Kondzio, ale to zadanie trzeba rozwiązać korzystając z interpretacji geometrycznej na osi liczbowej. Przeczytaj początek zadania.

kkkasiula: a ja wszystko rozumiem

Nei: By móc odnaleźć liczby w danym równaniu musi być minus − |x−liczba| = odległość. Tutaj mamy schemat |x+liczba| = odległość, a tak być nie może − trzeba to zamieić na minus, taka reguła. Czyli odwaracamy − z |x+liczba| = odległość , robimy |x−(−liczba)| = odległość. Dopiero można odczytać szukane liczby.

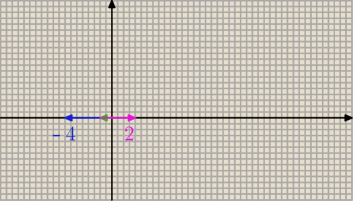
bolo: po prostu doprowadzamy do minusa w środku tak jak byśmy widzieli odległość 2 punktów na odcinku, albo wektorów o początku (0,0) i równoległy do osi , czyli punkt dalszy minus wcześniejszy, i tak |x+1| to inaczej |x−(−1)| i mamy odległość ich od (−1) wynosi 3 jednostki więc −1 −3 i −1 +3 stąd −4 i 2 mylę się?