Prosze o pomoc w zadaniu
ANKA: 
Oblicz objętość bryły obrotowej powstałej przez obrót dookoła osi OX wykresu funkcji:
| | √x | |
f(x) = |
| , x ∊ <1,2> |
| | x √x2 + 3x + 3 | |
Bardzo proszę o wyjaśnienie.
5 lip 23:51
Jack:
V=π∫f
2(x) dx na odpowiednim przedziale...
To prosty wzór... Szukałaś w necie (to pytanie bynajmniej nie jest oczywiste)?
5 lip 23:55
5 lip 23:57
ANKA: Tak, ale nie umiem policzyć tego przykładu...
5 lip 23:58
ANKA: A czemu π jest podniesione do kwadratu?
5 lip 23:59
Jack:
nie π, tylko (f(x) )
2.
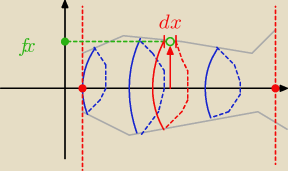
To działa mniej więcej tak, jak na rysunku. Bierzesz sobie mały kawałeczek wykresu, oznaczony
dx, i obracasz go dookoła osi OX. Powstaje Ci malutki walec o promieniu f(x) i wysokości dx.
Jego objętość do V= Pole podstawy RAZY wysokość = f
2(x)π * dx. Teraz zmieniając punkt
dostajesz inny walec i znów liczysz jego objętość. Całka oznacza w tym przypadku dodawanie
bardzo wielu takich objętości... Stąd to π, stąd kwadrat wartości funkcji i dx.
6 lip 00:10
Basia:
nie jest; to "2" to górna granica całkowania
6 lip 00:10
Basia:
Jack w linku, który podałeś to rzeczywiście na pierwszy rzut oka wygląda jak π12 i to
zmyliło Ankę
6 lip 00:12
Jack:
ok − myślałem że Anka pisze o wzorze z tego postu − przepraszam.
6 lip 00:13
ANKA: Dziękuje
6 lip 00:25
Jack:
na zdrowie!
6 lip 00:28