Lubelska Matura Probna dla klas pierwszych
Emily: Hejo wszystkim matematykom

Drodzy forumowicze mam ogromna prosbe czy moze ktorys z Was
posiada rozwiazania do zadan z tegorocznej lubelskiej matury probnej dla klas pierwszych na
poziomie rozszerzonym

Staralam sie wykonac te zadania jednak nie jestem pewna czy dobrze i
chcialam sie sprawdzic. Bardzo prosze o pomoc

25 cze 11:24
Jack:
Jak je przepiszesz , coś poradzimy

25 cze 11:43
Emily: ok, tylko dopiero wieczorem....dzieki za pomoc

25 cze 12:18
Emily: 1.Liczba a jest średnia arytmetyczna trzech liczb, a liczba b jest srednia arytmetyczna ich
kwadratow. Zapisz za pomoca a i b srednia arytmetyczna trzech par iloczynow tych liczb.
2.Niech m,n∊(nalezy) do rzeczywistych ujemnych wiec udowodnij , ze jezeli m−n=1 to prawdziwa
jest nierownosc 1m−1n≥4
3.Udowodnij ze 3 srodkowe rozcinaja trojkat na szesc czesci o rownych polach
4.Trojkat ABC podzielony jest przez dwie proste rownolegle do boku AC na trzy figury o rownych
polach. Oblicz na jakie czesci proste te podzielily bok AB=a
5.W prostokacie ABCD dany jest wierzcholek C (3:4) oraz AB=[4:3]. Znajdz rownania przekatnych
wiedzac , ze wierzcholek A nalezy do prostej x−y=5
26 cze 11:17
Emily: Bardzo prosze o pomoc, naprawde mi zalezy na sprawdzeniu tych rozwiazan

26 cze 11:18
Godzio:
Zaraz coś poradzimy

26 cze 12:16
Godzio:
Zad. 1
| 1 | |
| [ (x + y + z)2 − (x2 + y2 + z2) ] | | 2 | |
| | | |
| = |
| = |
| 3 | | 3 | |
26 cze 12:19
Godzio:
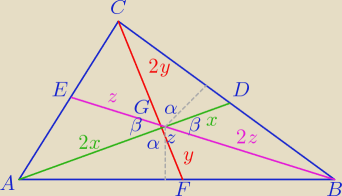
Zad. 3
Trójkąty AFG i FBG mają równe pola bo ich podstawy i wysokości na nie poprowadzone są równej
długości, analogicznie BDG i GDC oraz CEG i AEG,
| | 1 | |
Trójkąty AFG i GDC mają równe pola ponieważ [ korzystam z P = |
| absinα ] |
| | 2 | |
| | 1 | |
PAFG = |
| * 2x * y * sinα = xysinα |
| | 2 | |
| | 1 | |
PGDC = |
| * 2y * x * sinα = xysinα |
| | 2 | |
[ korzystam z faktu że środkowe w trójkącie przecinają się w stosunku 2 : 1 ]
Analogicznie pokazujemy, że FBG i CEG mają równe pola, i w ten sposób udowodniamy, że wszystkie
pola są równe
26 cze 12:30
TOmek: ciekawi mnie to 2. zadanie, cos nie chce mi wyjsc.
26 cze 12:33
TOmek: 1.
https://matematykaszkolna.pl/forum/97777.html
2. m,n∊ R
−
m−n=1
| 1 | | 1 | |
| − |
| ≥4 /*m zmieniamy znak bo "m" jest ujemne |
| m | | n | |
| | m | |
m− |
| ≤4m /*n zmieniamy znak bo "n" jest ujemne |
| | n | |
mn−m≥4mn
mn−3mn≥m
−2m(m−1)−m≥0
−2m
2+2m−m≥0
| | 1 | | 1 | |
−2m2+m≥0 "m" jest ujemne także wyrazenie |
| − |
| ≥4 to jest spełnione dla m,n∊R− |
| | m | | n | |
np: dla −1
−2*(−1)+(−1)≥0
2−1≥0
1≥0
Nie wiem czy przeszło by takie rozwiązanie, jak myslisz Godzio?

26 cze 12:38
TOmek: to jest chamstwo, aby zrobić zadanie "1". Potrzebny jest wzór (a+b+c)2 którego nie ma na
karcie wzorów, to jest nie fair!
26 cze 12:43
rumpek:
TOmek:
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ac
lub możesz skorzystać z (a+b)2 = a2 + 2ab + b2 wstawiając za "a = a + b", a z "b = c"
26 cze 13:09
ICSP: albo po prostu:
(a+b+c)(a+b+c) = a2 + ab + ac + ab + b2 + bc + ac + bc + c2 = a2 + b2 + c2 + 2ab + 2bc +
2ac
26 cze 13:11
Clay: Mnie natomiast intryguje 5. W sumie ciekawe zadanie zeby tylko jeszcze mi wyjsc chcialo zamiast
jakis glupot.....

26 cze 13:11
TOmek: zrobi ktos 2 zadanie?
26 cze 13:22
Jack:
Skoro AB=[4,3], to również DC=[4,3]. Stąd D=C−DC=(3,4)−[4,3]=(−1,1)
Prosta prostopadła do k:x−y=5 przechodząca przez punkt C ma wzór: l:y=−x+7. Przecina ona prostą
k w punkcie A(6,1) (układ równań z prostymi k i l).
Punkt B=A+AB=(6,1)+[4,3]=(10,4).
Teraz tylko proste wyznaczyć mają po dwa punkty...
26 cze 13:27
Jack:
Zad 2
m,n∊R
−
m−n=1 ⇒ n−m=−1
n−m≥4mn
−1≥4mn sprzeczność (bo mn>0).
Sprawdźmy, niech n=−2, m=−1 (m−n=−1+2=1):
−1+
12≥4
sprzeczność.
Polecenie chyba zostało błędnie przepisane...
26 cze 13:32
rumpek:
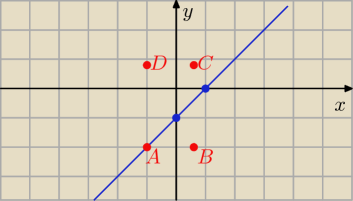
Rysujemy prostą x − y = 5
1
o. Prosta
−y = −x + 5 / * (−1)
y = x − 5
Przechodzi ona przez punkty
(0,−5) i (5,0)
Skoro punkt A leży na na proste y = x − 5 to określamy jakoś to.
Rysunek jest przykładowy i o wiele pomniejszony niż w rzeczywistości.
I teraz moje pytanie do dalszego rozwiązywania: Skoro A leży na prostej to musi być równa
odległość A i B od osi x. No i jakby sobie oznaczyć punkt B(3, y) bo teoretycznie B musi być
na tej samej linii co punkt C

Co wy na to

?
26 cze 13:35
Vax: 2) Znak nierówności powinien być skierowany w drugą stronę:
m−n=1 ⇔ m=n+1
−1 ≤ 4mn
4mn+1 ≥ 0
4n(n+1)+1 ≥ 0
4n
2+4n+1 ≥ 0
(2n+1)
2 ≥ 0
Co dla dowolnej liczby rzeczywistej będzie spełnione.
Pozdrawiam.
26 cze 13:36
TOmek: no i pasuje : ]
26 cze 13:37
rumpek: Ok,
Jack był szybszy

nawet wiem skąd to się wzięło chodź wektorów jeszcze nie miałem.
Trzeba będzie koniecznie o nich poczytać

26 cze 13:37
rumpek: Vax zrobiłem dokładnie tak samo jak ty

26 cze 13:38
TOmek: to "2" zadanko ładnie spieprzyłem

26 cze 13:41
Jack:

co cóż, trzeba było udowodnić − to udowodniłeś

26 cze 13:45
TOmek: jestem taki zajebisty, ze nawet zadanie które nie da sie udowodnic, potrafie udowodnić

26 cze 13:46
rumpek: Ten rysunek do zadania 5 nieźle "zdupcyłem" bo za bardzo dosłownie wziąłem sobie zadania do
serca

. Ale mam tylko pytanie do
jacka pewnie banalne i zapewne zapomniałem o jakieś
własności prostokąta, ale zapytam: na jakiej podstawie wyznaczamy prostą prostopadłą do y = x
− 5 przechodzącą przez punkt C?
26 cze 13:47
Jack:
Rozwiązanie Vaxa można było już wcześniej zakończyć...
...
−1 ≤ 4mn ← mn>0 więc teza zachodzi.
...
26 cze 13:49
Jack:
| | 1 | |
1. prostopadła do prostej k:y=a1x+b1 ma współczynnik a2=− |
| . Stąd l: |
| | a1 | |
| | 1 | |
y=− |
| x+b2 (b2 pozostaje nieznane). |
| | a1 | |
2. Mając dodatkowo punkt przez który ta prostopadła ma przechodzić wyznaczamy współczynnik b
2.
Faktycznie proste, pewnie zapomniałeś

26 cze 13:54
rumpek: O tym to pamiętam nieustannie

Tylko zastanawia mnie to, skąd wiedziałeś że prosta na której
leży punkt C jest prostopadła do prostej na której leży punkt A. Bo teoretycznie z rysunku to
nie wynika


26 cze 13:54
Jack:
mamy prostokąt

26 cze 13:55
Clay: rumpek....czyli wkoncu jak powinno wygladac rozw. zad. 5?/
26 cze 13:56
rumpek:
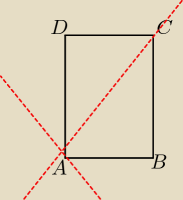

Całkiem możliwe.
26 cze 13:59
rumpek: napisałem wyżej
Patrz rozwiązanie Jacka 
26 cze 13:59
Godzio:
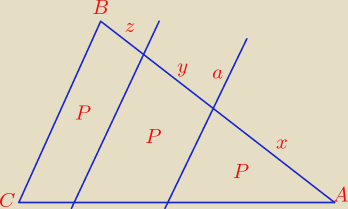
Zad. 4 Tego chyba nikt jeszcze nie robił,
P
ABC = 3P
x(
√2 − 1) = y
| √3 | |
| (x + x(√2 − 1) + z) = x |
| 3 | |
| √3 | | √6 | | √3 | | √3 | |
| x + x( |
| − |
| ) + |
| z = x |
| 3 | | 3 | | 3 | | 3 | |
z = x(
√3 −
√2)
x + x(
√2 − 1) + x(
√3 −
√2) = a
x(1 +
√2 − 1 +
√3 −
√2) = a
√3x = a
Przedstaw te długości w dowolnej postaci
26 cze 17:21
rumpek:
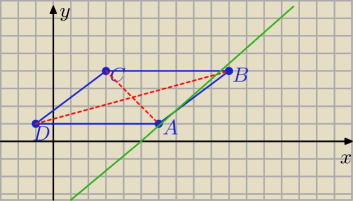
Się postarałem

Ale do konkretów: to jest ten rysunek z rozwiązania zadania 5, zadanie zrobione przez
Jacka.
Wyszły punkty A(6,1); B(10,4); C(3,4); D(−1,1). Niebieska linia to prosta y = x − 5 (i na tej
prostej leży punkt A − tak wynika z treści zadania). No i zostało policzone A w sposób:
1
o Znaleziono prostą prostopadłą do prostej y = x − 5 przechodzącą przez punkt C. Jest to
y = −x + 7
2
o Punkt A obliczono:
−x + 7 = x − 5
−2x = − 12 / (−2)
x = 6 i y = 1
A(6,1)
Na zadania.info znalazłem takie samo zadanie różniące się tylko danymi. Oto one:
http://www.zadania.info/d494/3365079
I tam mam już punkt A obliczony wynosi on według zadania.info
A(−4,−2).
I teraz chcę obliczyć tym samym sposobem co
Jack:
| | 1 | |
Tam jest prosta: x − 2y = 0 ⇒ −2y = − x / : (−2) ⇒ y = |
| x |
| | 2 | |
I punkt C(−2,2).
| | 1 | |
No to liczę prostą prostopadłą do prostej y = |
| x i przechodzącą przez punkt C(−2,2) |
| | 2 | |
a
1 * a
2 = −1
a
2 = −2
y = −2x + b
2 = −2 * (−2) + b
2 = 4 + b
b = −2
y = −2x − 2
Rozwiązując układ równań mam:
x = − 4x − 4
5x = − 4 / : 5
No i doszliśmy do momentu gdzie coś nie działa w tym sposobie

Co wy na to

?
26 cze 18:18
Godzio:
"Znaleziono prostą prostopadłą do prostej y = x − 5 przechodzącą przez punkt C"
Nie rozumiem dalszej części, dlaczego ta prosta miałaby dać z prostą y = −x + 7 punkt A ?
26 cze 18:36
rumpek: Mnie się pytasz? Sam tego nie rozumiem jack tak napisał w poście o godzinie 13:27
26 cze 18:39
rumpek: według mnie to w ogóle nie tak jak jack pokazał tylko jak na zadania.info
26 cze 18:40
Emily: Bardzo Wam dziekuje za pomoc , jestem ogromnie wdzieczna

przyznam ze niektore rozwiazania
zaskakuja mnie pomyslowoscia sama nie wpadlam na takie rozwiazanie

26 cze 19:41
Haq:
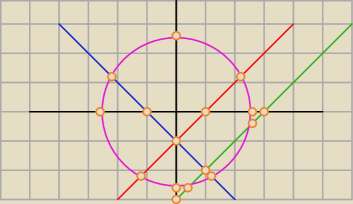
27 cze 09:38
 Drodzy forumowicze mam ogromna prosbe czy moze ktorys z Was
posiada rozwiazania do zadan z tegorocznej lubelskiej matury probnej dla klas pierwszych na
poziomie rozszerzonym
Drodzy forumowicze mam ogromna prosbe czy moze ktorys z Was
posiada rozwiazania do zadan z tegorocznej lubelskiej matury probnej dla klas pierwszych na
poziomie rozszerzonym Staralam sie wykonac te zadania jednak nie jestem pewna czy dobrze i
chcialam sie sprawdzic. Bardzo prosze o pomoc
Staralam sie wykonac te zadania jednak nie jestem pewna czy dobrze i
chcialam sie sprawdzic. Bardzo prosze o pomoc 




 Zad. 3
Trójkąty AFG i FBG mają równe pola bo ich podstawy i wysokości na nie poprowadzone są równej
długości, analogicznie BDG i GDC oraz CEG i AEG,
Zad. 3
Trójkąty AFG i FBG mają równe pola bo ich podstawy i wysokości na nie poprowadzone są równej
długości, analogicznie BDG i GDC oraz CEG i AEG,


 Rysujemy prostą x − y = 5
1o. Prosta
−y = −x + 5 / * (−1)
y = x − 5
Przechodzi ona przez punkty
(0,−5) i (5,0)
Skoro punkt A leży na na proste y = x − 5 to określamy jakoś to.
Rysunek jest przykładowy i o wiele pomniejszony niż w rzeczywistości.
I teraz moje pytanie do dalszego rozwiązywania: Skoro A leży na prostej to musi być równa
odległość A i B od osi x. No i jakby sobie oznaczyć punkt B(3, y) bo teoretycznie B musi być
na tej samej linii co punkt C
Rysujemy prostą x − y = 5
1o. Prosta
−y = −x + 5 / * (−1)
y = x − 5
Przechodzi ona przez punkty
(0,−5) i (5,0)
Skoro punkt A leży na na proste y = x − 5 to określamy jakoś to.
Rysunek jest przykładowy i o wiele pomniejszony niż w rzeczywistości.
I teraz moje pytanie do dalszego rozwiązywania: Skoro A leży na prostej to musi być równa
odległość A i B od osi x. No i jakby sobie oznaczyć punkt B(3, y) bo teoretycznie B musi być
na tej samej linii co punkt C  Co wy na to
Co wy na to  ?
?
 nawet wiem skąd to się wzięło chodź wektorów jeszcze nie miałem.
Trzeba będzie koniecznie o nich poczytać
nawet wiem skąd to się wzięło chodź wektorów jeszcze nie miałem.
Trzeba będzie koniecznie o nich poczytać 


 co cóż, trzeba było udowodnić − to udowodniłeś
co cóż, trzeba było udowodnić − to udowodniłeś 

 . Ale mam tylko pytanie do jacka pewnie banalne i zapewne zapomniałem o jakieś
własności prostokąta, ale zapytam: na jakiej podstawie wyznaczamy prostą prostopadłą do y = x
− 5 przechodzącą przez punkt C?
. Ale mam tylko pytanie do jacka pewnie banalne i zapewne zapomniałem o jakieś
własności prostokąta, ale zapytam: na jakiej podstawie wyznaczamy prostą prostopadłą do y = x
− 5 przechodzącą przez punkt C?

 Tylko zastanawia mnie to, skąd wiedziałeś że prosta na której
leży punkt C jest prostopadła do prostej na której leży punkt A. Bo teoretycznie z rysunku to
nie wynika
Tylko zastanawia mnie to, skąd wiedziałeś że prosta na której
leży punkt C jest prostopadła do prostej na której leży punkt A. Bo teoretycznie z rysunku to
nie wynika 



 Całkiem możliwe.
Całkiem możliwe.

 Zad. 4 Tego chyba nikt jeszcze nie robił,
PABC = 3P
Zad. 4 Tego chyba nikt jeszcze nie robił,
PABC = 3P
 Się postarałem
Się postarałem  Ale do konkretów: to jest ten rysunek z rozwiązania zadania 5, zadanie zrobione przez
Jacka.
Wyszły punkty A(6,1); B(10,4); C(3,4); D(−1,1). Niebieska linia to prosta y = x − 5 (i na tej
prostej leży punkt A − tak wynika z treści zadania). No i zostało policzone A w sposób:
1o Znaleziono prostą prostopadłą do prostej y = x − 5 przechodzącą przez punkt C. Jest to
y = −x + 7
2o Punkt A obliczono:
−x + 7 = x − 5
−2x = − 12 / (−2)
x = 6 i y = 1
A(6,1)
Na zadania.info znalazłem takie samo zadanie różniące się tylko danymi. Oto one:
http://www.zadania.info/d494/3365079
I tam mam już punkt A obliczony wynosi on według zadania.info A(−4,−2).
I teraz chcę obliczyć tym samym sposobem co Jack:
Ale do konkretów: to jest ten rysunek z rozwiązania zadania 5, zadanie zrobione przez
Jacka.
Wyszły punkty A(6,1); B(10,4); C(3,4); D(−1,1). Niebieska linia to prosta y = x − 5 (i na tej
prostej leży punkt A − tak wynika z treści zadania). No i zostało policzone A w sposób:
1o Znaleziono prostą prostopadłą do prostej y = x − 5 przechodzącą przez punkt C. Jest to
y = −x + 7
2o Punkt A obliczono:
−x + 7 = x − 5
−2x = − 12 / (−2)
x = 6 i y = 1
A(6,1)
Na zadania.info znalazłem takie samo zadanie różniące się tylko danymi. Oto one:
http://www.zadania.info/d494/3365079
I tam mam już punkt A obliczony wynosi on według zadania.info A(−4,−2).
I teraz chcę obliczyć tym samym sposobem co Jack:
 Co wy na to
Co wy na to  ?
?
 przyznam ze niektore rozwiazania
zaskakuja mnie pomyslowoscia sama nie wpadlam na takie rozwiazanie
przyznam ze niektore rozwiazania
zaskakuja mnie pomyslowoscia sama nie wpadlam na takie rozwiazanie 
