trapezy
Miśka: W trapezie ABCD przekątne AC i BD przecinaja się w punkcie O. Pole trójkąta ABO jest równe
32cm2 , a pole trójkąta CDO 2cm2. Oblicz:
a) stosunek długości podstaw ICDI : IABI
b) Oblicz pole trapezu ABCD
9 cze 12:23
krystek: Z pΔ(aBO) wyznacz długośc AB
Z PΔ(CDO) wyznacz długość CD i masz odp na podp.a) A potem już policzysz P trapezu
9 cze 13:19
hwdtel:
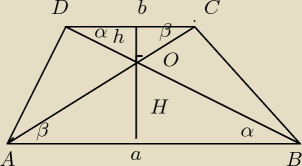
| | h | | H | |
ΔAOB∼ΔCOD : |
| = |
| ; hb2=S1=(2cm2) ; Ha2=S2=(32 cm2)
|
| | b | | a | |
| | √S1 | | √S1 | |
P = 12(a+b)H = 12(a+a |
| )(H+H |
| ) =
|
| | √S2 | | √S2 | |
(
√S1 +
√S2)
2 = 42 cm
2
11 cze 11:37
hwdtel i x3:
Oczywiście wynik wynosi 2+2*8+32 cm2
11 cze 11:42
Mick: Z jakiego zbioru jest to zadanie ?
7 paź 14:15
wera: mógłby ktoś to wytłumaczyć
nie wiem skąd się to wzieło−> (√S1 + √S2)2 = 42 cm2
mógłby
ktos to rozpisać
help
15 kwi 23:04
wera: wynik ma być 50
15 kwi 23:13
15 kwi 23:13
Eta:
P(tr}= (√P1+√P2)2 = (√32+√2)2= (4√2+√2)2= (5√2)2= 50
15 kwi 23:15
wera: dzieki
15 kwi 23:22