nie wiem jak sie za to zabrac :( marti: W trapezie ABCD o podstawach AB i CD punkt O jest punktem wspólnym przekątnych. Oblicz pole trapezu wiedzac ze pole trojkata ABO jest rowne 5 a pole trojkata CDO jest rowne 4. Bardzo prosze o pomoc:( czy mozna to zrobic z podobienstwa trojkatow?

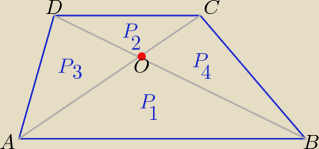
Eta: P₁=5 , P₂= 4 Wiesz ,że P₃=P₄ i taki wzorek P(tr)= (√P₁+√P₂)² , P₃=P₄= √P₁*P₂ = √20= 2√5 P(tr)= (√5+2)²= 9+√5 [j²]

marti: Proszę chociaż kilka wskazówek żeby samodzielnie to rozwiązać, bardzo mi zależy..

marti: Dziękuje!

marti: a ten wzor to do wszystkich trapezow mozna stosowac, zawsze?

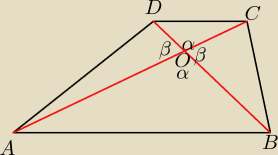
Basia: tr.AOB i tr.COD są podobne skala podobieństwa = k

	5
k2 =
	4

	√5
k =
	2

OD = x ⇒ OB = kx OC = y ⇒ OA = ky P_COD = x*y*sinα musimy obliczyć pole tr.AOD i tr.BOC

	√5
PAOD = ky*x*sinβ = k*x*y*sin(180−α) = k*x*y*sinα = k*PCOD =		*4 = 2√5
	2

P_BOC = kx*y*sinβ = 2√5 P = 4+5+2√5+2√5 = 9+4√5

Eta: Wyprowadzenie tego wzoru: P(tr)= P₁+P₂+P₃+P₄= P₁+2P₃+P₂ P(tr)= (√P₁+√P₂)²= P₁+2√P₁*P₂+P₂= P₁+P₂+2P₃ , dla P₃=P₄=√P₁*P₂

Eta: Chochlik "pożarł" mi 4 P(tr)= 9+4√5

marti: Bardzo dziękuję Basia i Eta , juz zrozumiałam

Eta: No to jeszcze jeden... taki P(tr)= (k+1)²*P₂ , k>0 skala podobieństwa trójkątów ABO i CDO P₁= k²*P₂ , P₃=P₄= k*P₂ P(tr)= P₁+P₃+P₄+P₂= k²*P₂+2k*P₂+P₂= (k²+2k+1)*P₂= (k+1)²*P₂

	5		√5
k2=		⇒k=
	4		2

	√5
P(tr)= (		+1)2*4= ......... 9+4√5
	2

Eta: Napisałam tylko dlatego,że "kocham" te dwa wzorki

Ku2ja: Eta, a skąd wiemy że P₃ = P₄ ?

dro: Eta, Czy jest gdzieś w sieci ten wzór na trapez wyprowadzony? Nie mogę nigdzie znaleźć skąd to się wzięło.

dro: Chodzi mi o wzory P(tr)= (√P1+√P2)2 , P3=P4= √P1*P2, potrzebuję uczciwego wyprowadzenia tych wzorów.