.
Kasia: 1. W równoległoboku o obwodzie 40 cm przekątne są dwusiecznymi kątów, a ich długości mają się
do sobie jak 3:4. Oblicz długości tych przekątnych.
2. W równoległoboku ABCD wysokość DE ma 8 cm i dzieli bok AB na odcinki długości : I AE I = 4,5
cm, I EB I = 6 cm. Oblicz długości przekątnych tego równoległoboku.
3. Na trapezie opisano okrąg o promieniu długości 25 cm. Dłuższa podstawa trapezu jest średnicą
tego okręgu. Wiedząc, że przekątna trapezu ma długość 40 cm, oblicz obwó tego trapezu.
Bardzo prosze o pomoc, nie moge sobie z nimi poradzić
geometria jest moją piętą Achilesa
4 cze 22:55
4 cze 23:01
Kasia: dzięki Godzio! Zaczne szukać zanim dam zadanie
tylko mam pytanie co do zad. 3 bo nie miałam tw. cosinusów itd więc jak to zrobić inaczej żeby
już na końcu wyliczyć tą krótszą podstawę?
4 cze 23:06
Godzio:
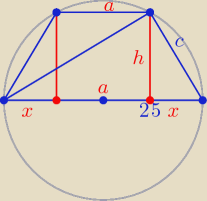
40
2 + c
2 = 50
2
c
2 = 900
c = 30
40
2 = (50 − x)
2 + h
2
h
2 + x
2 = c
2 ⇒ h
2 = c
2 − x
2
1600 = 2500 − 100x + x
2 + 900 − x
2
x = 18
a = 50 − 2x = 50 − 36 = 14
L = 2c + 50 + a = ...
4 cze 23:14
Kasia: ale jak wyliczyłeś tutaj h ? skoro masz tam niewiadomą x i h więc nie rozumiem..
4 cze 23:27
Godzio:
A gdzie tu jest wyliczone h ? Nie trzeba więc nie liczę
5 cze 00:14
Kasia: to w takim razie po co te dwie linijki gdzie jest wzmianka o h? i nie rozumiem tej linijki,
która się zaczyna od 1600.. : (
5 cze 00:26
Godzio:
402 = (50 − x)2 + h2 gdzie h2 = c2 − x2 = 900 − x2
1600 = 2500 − 100x + x2 + 900 − x2
Teraz jasne ?
5 cze 00:27
Kasia: tak. wybacz, ale nie zrozumiałam o co Ci chodziło, teraz już wszystko stało się jasne
jeszcze raz bardzo dziękuję
5 cze 00:31
Godzio:
Wybaczam
5 cze 00:39