Matura Rozszerzona. Matt: Zapraszam do zadań z matury rozszerzonej w tym temacie aby był jakis porządek na forum. Link do arkusza: http://www.cke.edu.pl/images/stories/00002011_matura/R/pr_matematyka.pdf PS. Prawdopodobnie uwaliłem rozszerzenie.

Kuba: Zadanie 1. Uzasadnij, że dla każdej liczby całkowitej k liczba k⁶ − 2k⁴ + k² jest podzielna przez 36. k⁶ − 2k⁴ + k² k⁶ − k⁴−k⁴ + k² k⁴(k²−1)−k²(k²−1)= (k⁴−k²)(k−1)(k+1)= (k²−k)(k²+k)(k−1)(k+1)= (k−1)(k+1)(k−1)(k+1)k²= k²(k−1)²(k+1)²= [k(k−1)(k+1)]² Słownie: Iloczyn trzech kolejnych liczb całkowitych jest podzielny przez 6 stąd kwadrat tego iloczynu jest podzielny przez 36. Ja tak uzasadniłem nie wiem czy dobrze, nie bijcie!

Kuba: Zadanie 2

	a		b
Uzasadnij, że jeżeli a ≠ b , a ≠ c , b ≠ c i a + b = 2c , to		+		=2
	a−c		b−c

a(b−c)+b(a−c)
	=2
(a−c)(b−c)

ab−ac+ab−bc)
	=2
(a−c)(b−c)

2ab−ac−bc)
	=2
(a−c)(b−c)

2ab−c(a+b)
	=2
(a−c)(b−c)

2ab−2c2
	=2
(a−c)(b−c)

2ab−2c²=2(a−c)(b−c) 2ab−2c²=2ab−2ac−2bc+2c² −4c²=−2ac−2bc −4c²=−2c(a+b) −4c²=−2c(2c) −4c²=−4c² L=P Mam nadzieje że dobrze, znowu nie bijcie!

Kosmos: haa ja tak samo zrobiłem

Kosmos: ale Godzio chyba nas zbije

Kuba: Zadanie 3 Wyznacz wszystkie wartości parametru m , dla których równanie x² − 4mx − m³ + 6m² + m − 2 = 0 ma dwa różne pierwiastki rzeczywiste x₁ , x₂ takie, że (x₁−x₂)²<8m+8 I − Δ>0 II − (x₁−x₂)²<8m+8 I − 16m²+4m³−24m²−4m+8>0 4m³−8m²−4m+8>0 4m(m²−1)−8(m²−1)>0 (m−1)(m+1)(4m−8)>0 m∊(−1,1)u(2,+∞) II − {x₁}²−2x₁x₂+{x₂}²+2x₁x₂−2x₁x₂<8m−8 (x₁+x₂)²−4x₁x₂−8m+8<0 16m²−4(− m³ + 6m² + m − 2)−8m−8<0 16m²+4m³ − 24m² − 4m + 8−8m−8<0 4m³ −8m² −12m<0 m³ −2m² −3m<0 m(m² −2m −3)<0 Δ=4+12 m₁=3 m²=−1 m(m+1)(m−3)<0 m∊(−∞,−1)u(0,3) I i II m∊(2,3)

Patryks: To ja mam podobnie jak Wy Oby dobrze

M4ciek: 3 mam inaczej : m∊(0,1) ∪ (2,3)

Kuba: Zadanie 4 Rozwiąż równanie 2sin²x − 2sin²x cos x = 1− cos x w przedziale <0,2π> 2−2cos²x−2(cosx−cos³x)−1+cosx=0 2−2cos²x−2cosx+2cos³x−1+cosx=0 2cos³x−2cos²x−cosx+1=0 2cos²x(cosx−1)−(cox−1)=0 (cosx−1)(√2cosx−1)(√2cosx+1)=0 cosx=1 x₁=0π x₂=2π cosx=√2/2 x₃=π/4 x₄=7/4π cosx=−√2/2 x₅=3/4π x₆=5/4π

wewe: yeah 3 zadania poki co mam tak samo

ICSP: łoo trygonometrię ma dobrze xD Chyba pierwszy raz w życiu W zadaniu z parametrem do dowaliłem coś takiego

	1 + √17
m ∊ (1 ;		)
	2

rumpek: Kuba w zadaniu 3: m∊(0,1)U(2,3)

rumpek: ICSP ile będzie ?

Kuba: Zadanie 5 O ciągu (x_n ) dla n ≥1 wiadomo, że: a) ciąg ( a_n) określony wzorem 3^x_n dla n ≥1 jest geometryczny o ilorazie q = 27 . b) x₁+x₂...x₁0=145. Oblicz x₁ a₂=3^x₁*3³ 3^x₂=3^x₁*3³ x₂=x₁+3 a₃=3^x₁*(3³)² x₃=x₁+6 x₃−x₂=r r=3 a₁0=.... x₁0=x₁+9r S_n=2x₁+9r/2 *10 145= 2x₁+9r *5 2x₁=2 x₁=1 Dalszy ciąg zaraz, bo fakty lecą

ICSP: podstawa 100% rozszerzenie około 70%

ICSP: x₁ = 1 k***a z******y jestem

Kuba: ajj faktycznie w zadaniu 3, no to mi punkt ukradną

M4ciek: x₁ jest

M4ciek: Pytanie do ekspertow : 1.Czy dostane punkt za wypisanie zbioru Ω ? Ω = 7² = 49 Zbior A zle wypisalem .... i mam P(A) za male 2.Sa punkty za rysunki ? 3.Czy jak mi wyszlo z graniastoslupem X_w = 1 I na koncu policzylem f(1) = 12 i dalem odp. bok = 12 to czy mam punkty do czasu wyliczenia (prawidlowego x_w = 1 i odejma mi tylko za odpowiedz?

Matt: 1. Sądzę że tak. Ja też mam Ω dobrą A wyliczenia złe.. (Zapomniałem że 3+3=6 xD )

kamis: 7. x² + y² + 2x − 2y − 3 = 0 Po przekształceniu: (x + 1)² + (y − 1)² = 5 Współrzędne środka S =(−1, 1) Długość promienia r = √5 Przez punkty B i C oznaczmy punkty styczności. Wówczas z twierdzenia o dwóch stycznych do okręgu: |BA| = |CA| |SA| = √10 Z tw. Pitagorasa dla ΔSBA |BA|² + r² = |SA|² |BA|² = 5 |BA| = √5 Oznacza to, że czworokąt ABCS jest kwadratem (boki tej samej długości i kąt 90 stopni, pomiędzy promieniem, a styczną), zatem kąt między stycznymi jest równy 90 stopni.

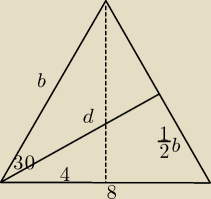
Kuba: b=8√3/3 1/2b=8√3/6

	192		128√3
d2=64+		−		*√3/2=
	36		6

	192
d2=64−32+
	36

hmm na maturze wyszło mi widocznie źle ....

	192
d=√32+
	36

	1344
d=√
	36

rumpek: Matko co to

rumpek: https://matematykaszkolna.pl/forum/94611.html Tam już rozwiązałem to tylko usuń niewymierność i wychodzi prawidłowy wynik

Vizer: Dobrze mu wyszło

rumpek:

4√21
	powinno wyjść
3

Vizer:

	112
wiesz myśle, że jak by zostawił √		to by nie ucieli punktow
	3

Kuba: mam nadzieje że za błędy w liczeniu odejmują tylko po 1 punkcie...

luk18: Ja też...

kamis: 12. P(A ∩ B') = P(A) + P(B') − P(A ∪ B') P(A ∩ B') = 1,2 − P(A ∪ B') 1,2 − P(A ∪ B') ≤ 0,3 − P(A ∪ B') ≤ −0,9 |* (−1) P(A ∪ B') ≥ 0,9 P(A) = 0,9 P(A ∪ B') ≥ P(A), więc P(A ∪ B') ≥ 0,9

maturka: zad. 12 P(B')=0,3 Zatem P(A∩B') musi być mniejszy lub równy 0,3 (no bo nie może być większy, iloczyn to część wspólna zbiorów) ja to tak zrobiłem a wcześniej przez 20min męczyłem się innymi sposobami xD

wewe: @matura ja dokladnie tak samo, patrzyles moze gdzies czy to jest dobrze zrobione ?

Maturzysta: podstawa zaj****/bardzo łatwa... <90% to hańba. rozszerzenie zupełnie inna bajka... powyżej 70% trzeba było się wykazać wiedzą...

Patryks: Jak myślicie ile bedzie trzeb miec około punktów z maty żeby na agh się dostac ? Na powiedzmy robotyke lub inny kierunek ?

Epo: Z podstawy około 100, a rozszerzona 85. Oczywiście bez rozszerzonego angielskiego się nie dostaniesz

M4ciek: Policzy to ktos : Oblicz, ile jest liczb ośmiocyfrowych, w zapisie których nie występuje zero, natomiast występują dwie dwójki i występują trzy trójki.

Vizer:

8 3		5 2
	*		*73

M4ciek: Rozwiazalbys do konca?

Vizer:

8*7*6		5*4
	*		*343=56*10*343=192080
6		2

uhu: http://www.agh.edu.pl/pl/kandydaci/informacje-podstawowe/najczesciej-zadawane-pytania/progi-punktowe.html masz na agh ale moim zdaniem w tym roku progi spadną bo matura była dużo trudniejsza

Epo: To stare progi. W tamtym roku na robotyke 908.

M4ciek: Pytanie do ekspertow : 1.Sa punkty za rysunki ? 2.Czy jak mi wyszlo z graniastoslupem Xw = 1 I na koncu policzylem f(1) = 12 i dalem odp. bok = 12 to czy mam punkty do czasu wyliczenia (prawidlowego xw = 1 i odejma mi tylko za odpowiedz?

;;: czyli w tym roku jeszcze niższe

Kuba: jakby ktoś chciał i mógł spojrzeć byłbym wdzięczny, moje rozwiązanie zadania z prawdopodobieństwa taka trochę kpina, nie bijcie za to ale powiedzcie czemu to jest źle http://img197.imageshack.us/i/prawds.jpg/

bart: mozna tak bierzemy max prawdopodobienstwo.. P(AuB')=1 P(AuB')=P(A)+P(B)−P(AnB') 1=0,9+0,3−P(AnB') P(AnB')=0,2 − maxymalne a 0,2≤0,3 tak na chlopski rozum

rumpek: Ją już odpowiedzi na zadania.info

bart: link!

rumpek: Płatny!

Kuba: http://www.zadania.info/67076 ma ktoś konto? niech tu wrzuci, ja nie jestem taki bogaty

rumpek: w sensie aby dostać się tam trzeba sms wysłać lub miec abonament

bart: pf.. ale sobie zarobia dzisiaj

xox: mógłby mi ktoś wytłumaczyć zadanie 9? bo coś chyba mi sie z......ło. (prymitywnym sposobem) ∟∟∟∟∟∟∟∟ <− liczba 8−cyfrowa. dwie dwójki i trzy trójki. Pierwszą dwójkę mogę ustawić na 8 sposobów. Drugą dwójkę mogę ustawić na 7 sposobów. Pierwszą trójkę mogę ustawić na 6 sposobów. Drugą trójkę mogę ustawić na 5 sposobów. Trzecią trójkę mogę ustawić na 4 sposobów. i tu ZAĆMIENIE = 8*7*6*5*4 = 6720 teraz DODAĆ czy POMNOŻYĆ? chyba pomnożyć. szkoda, że przekonano mnie o tym po fakcie −_____________− i dalej: pozostałych liczb zostało: {1, 4, 5, 6, 7, 8, 9} = 7³ = 343 można je ustawić na 3! sposobów 6 * 343 + 6720 = 2058 + 6720 = 8778. Po wymnożeniu = 6720 * 2058 = 13 829 760 O____ o

rumpek: bart podaj maila to ci wyślę

rumpek: Tylko coś im chyba 6 kuleje, napisałem już do nich. Większość ma odpowiedź

4√21		4√15
	a oni mają
3		3

bart:

Patryks: Przyglądając się diagramowi możemy zauważyć, że P (A ∩ B′) = P (A ∖ B) = P (A )− P (A ∩ B ) = 0,9 − P(A ∩ B). Musimy więc oszacować P(A ∩ B ) . Korzystamy z niezastąpionego wzoru na sumę zdarzeń P(A ∪ B) = P (A )+ P (B) − P (A ∩ B ). W szczególności 1 ≥ P(A ∪ B) = P (A )+ P(B )− P (A ∩ B ) = 0,9+ 0,7 − P(A ∩ B) − 0,6 ≥ −P (A ∩ B). Mamy stąd ′ P (A ∩ B ) = 0,9 − P (A ∩ B ) ≤ 0,9− 0,6 = 0,3.

Bogdan: Zadanie 2 z poziomu rozszerzonego (treść wyżej podał Kuba). Proponuję takie rozwiązanie:

	a + b
a + b = 2c ⇒ c =
	2

a		b		a		b
	+		=		+		=
a − c		b − c		a + b   a −   2		a + b   b −   2

	2a		2b		2a		2b		2(a − b)
=		+		=		−		=		= 2
	2a − a − b		2b − a − b		a − b		a − b		a − b

bart: kurcze.. juz mysalem ze znalazlem u Bogdana bląd ale nieeee.. nieeeee..

kururugi: a ile dostane pkt jak obliczyłem b' i powiedzialem ze jego cześć wspolna z A ne może być większ od 0,3

rumpek: Bogdan tak samo zrobiłem w komentarzach: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=2997

kururugi: a w zadaniu 2 mogłem rozpocząć od przekształcania równości po prawej stronie? na końcu wyszło mi to z lewej

wolfy: ja proponuje jeszcze inne: a=2c−b po paru przeksztalceniach

−2(b−c)2
	=2 (czy jakos tak L=P ^^ )
(b−c)(c−b)

bart: no jak powiedzailes to nic.. jakbys napisal to moooooze..

bart: @kuruurgi tak

kururugi: aha a w zadaniu 11 wyszło może 8/√82 strasznie sie stresuje bo niedużo mi brakuje do 80 ;>

xox: mógłby ktoś to 9 skorygować?

Bogdan: Zadanie 4. 2sin²x − 2sin²xcosx = 1 − cosx dla x∊<0, 2π>.

	1
2sin2x(1 − cosx) − (1 − cosx) = 0 ⇒ 2(1 − cosx)(sin2x −		) = 0
	2

cosx = 1 ⇒ x = 0 lub x = 2π lub

	√2		√2		√2		√2
(sinx −		)(sinx +		) = 0 ⇒ sinx =		lub sinx = −
	2		2		2		2

	1		3		5		7
x =		π lub x =		π lub x =		π lub x =		π
	4		4		4		4

	1		3		5		7
Odp.: x∊{0,		π,		π,		π,		π, 2π}
	4		4		4		4

kururugi: panie bogdanie można 11 zrobić?

Bogdan: Do rumpek − nie zauważyłem Twojego wcześniejscego wpisu

smiglo92: Witam! Nie sądzicie, że w zadaniu z iloscią liczb ośmiocyfrowych rozwiązanie bedzie o wiele trudniejsze, bo przeciez moze byc więcej tych dwojek i trójek w zapisie dziesiętnym, które trzebaby dodac.

bart:

	4
mi wyszlo		√82 ale wiem ze po drodze mialem taki wynik ale to byla ktoras z
	41

wysokosci.. mojego wyniku nie jestem pewny

bart: @smiglo92 no to mozna bylo dwojako rozumiec to jest wlasnie prawdopodobienstwo..

kururugi: nie rozwiązanie wyżej jest dobrze. spędziłem na tym zadaniu 15 minut i warunki z 2 i 3 mam tak samo a reszte walnąłem ale tu jest dobrze

smiglo92: ja uczyłem sie na matematyce, że jak nie ma słowa dokładnie to rozwaza sie rozne przypadki

bart: ale to by bylo za trudne, tj zbyt czasochlonne

kururugi: ten wynik jest chyba taki sam jak u mnie, ale wyciągnięta niewymierność z mianownika odejmą punkty?

smiglo92: Zdenerwowalbym sie jakby mi tego nie uznali bo w ostatniej chwili zmienialem

bart: nie wyciagnales? nie jestem egzaminatorem ale raczej za takie bzdety nie odejma

bart: @smiglo92 a masz taki jak my?

gawi: a czemu nie mogę jak wyłącze te 2 sin kwadrat podzielic przez 1−cos alfa i bede miala ze 2 sin kwadrat =1?

Kuba: bo to zawęża liczbę rozwiązań bodaj do 3 a powinno być ich 6

smiglo92: Nie no wynik jest zupelnie inny.

gawi: nie no wyszlo mi 4

kururugi: nie wyciągnięte ale ważne że sunus dobry

bart: @gawi bo tracisz wtedy rozw

gawi: jakki zal...to mi nic nie zalicza?:(

bart: zalicza Ci cos napewno jakies 2 pkt stracisz

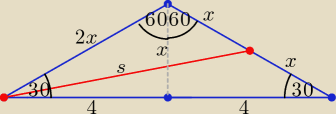
Bogdan: Zadanie 6. Korzystając z własności trójkąta prostokątnego o katach ostrych 60^o i 30^o otrzymujemy:

	√3		4
x√3 = 4 / *		⇒ x =		√3
	3		3

Długość środkowej s wyznaczamy z wykorzystaniem twierdzenia cosinusów:

gawi: oby zdac..

Kuba: rozszerzenie? gwarantuje ci że zdałeś

gawi: moge napisac co napisaŁAM xD i wqtedy ogarniemy czy zdam hmm?

Hmmm: dlaczego kat wyszedl prosty przy tych prostych?

Hmmm: wspolczynnik prosty kierunkowej wyszedl 1/2 wiec to sa 22 stopnie 180− 2*22=136 stopni przeciez −−− dlaczego 90 sie pytam?>:(

Rivi: Ale miałeś kąt pomiędzy dwoma prostymi (stycznymi) jedna miała 1/2 druga −2 1/2*−2=−1 więc były one prostopadłe

tomek: ja rozwiązałem to zadanie z liczba osmiocyfrową podobnie jak te z GW ze środy co w tamtym tygodniu była na 3 przypadki kiedy na poczatku jest 2, 3 lub inna cyfra niz 2 i 3 a co do tych funkcji jak podzieliłem przez 1−cosx to duzo mi odejmą punktów za to zawęzenie rozwiazań?

	π		3π
wyszło mi ze x1 =		i x2 =
	4		4

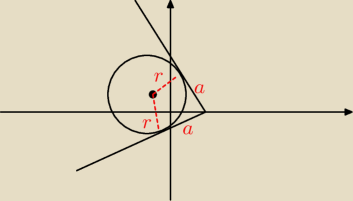
Kuba: a na przykład między r i a jest kąt prosty bo to warunek styczności i skoro to jest czworotkąt to suma kątów musi wynosić 360−180/2=90 czy to zbyt naciągane? zbyt naciągane, wiedziałem

maturka: @Kuba: niestety, ale same kąty proste jak podajesz to warunki na powstanie deltoidu, niekonieczine kwadratu...

Patryks: sory ziomki... ale chyba będziemy rowy kopać...

tomek: ale to podzieliłeś sume kątów przy S i A przez 2, a nigdzie nie wyliczyłeś ze to jest kąt prosty

tomek: no same się nie wykopią

bart: dla mnie wykopice, zebym mial gdzie lezec, jak juz skoncze te wszystkie egzaminy chyba we wrzesniu sie obudze

A: A co powiecie na to: Zadanie 9

	8 2		6 3
Jest		sposobów na rozmieszczenie 2, i		sposobów na rozmieszczenie 3.

Zostały 3 'miejsca' do wypełnienia. I teraz są 3 przypadki: 1. pozostałe trzy cyfry są takie same 2. 2 cyfry z tych pozostałych są takie same 3. każda cyfra z tych trzech jest inna

	8 2		6 3		8 2		6 3
w pierwszym przypadku tych liczb jest		*		*7*1*1, w drugim		*		*7*6*1, w

	8 2		6 3
trzecim		*		*7*6*5

Po zsumowaniu powinno wyjść 145040.

Krz: No powiedzmy, ze zdałem Jak na początek przygotowań do rozszerzonej 2 tygodnie przed egzaminem to miedzy 30 a 40 nie jest chyba tragedia Chce ktoś odpowiedzi z zadania.info? bo pare dni temu w akcie desperacji wykupiłem u nich abonament zdziercy

Michał: Ja bardzo chętnie

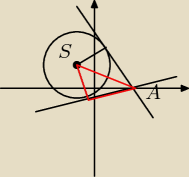
Krotton: Pomiędzy styczną a promieniem mamy kąt prosty. Możemy więc po prostu wyliczyć sinus α/2 korzystając z trójkąta zaznaczonego na czerwono. sin(α/2) = r / |SA| α/2 wynosi 45 lub 135 stopni, a więc α − 90 lub 270. Drugi wynik jednak odrzucamy, gdyż chodzi nam o kąt wypukły.

Eta: @ do b W/g mnie, to cyfry 3 i 2 i 0 już nie mogą się powtarzać na pozostałych trzech miejscach zatem wynik jest:

	8 3		6 2
		*		*73 = 560*73

Co Ty na to?

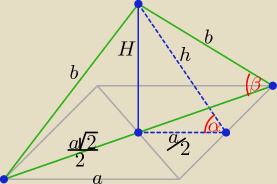
Bogdan: Zadanie 11. α, β ∊ (0^o, 90^o)

a√2		6		1		a		6
	=		/ *		⇒		=
b		5		√2		b		5√2

a√2		6		a   √2 2		3		3
	=		⇒		=		⇒ cosβ =
b		5		b		5		5

	4		H		4		4
sinβ =		⇒		=		⇒ H =		b
	5		b		5		5

1   a 2

1   a 2

5

a

5

6

ctgα =

=

=

*

=

*

H

4   b 5

8

b

8

5√2

	3√2
ctgα =		⇒ sinα = ...
	8

	π
Można też wyprowadzić zależność: cos		= tgβ * ctgα,
	n

gdzie: n to liczba boków n−kąta foremnego bedącego podstawą ostrosłupa prawidłowego, β to miara kąta nachylenia krawedzi bocznej do płaszczyzny podstawy, α to miara kąta nachylenia ściany bocznej do płaszczyzny podstawy.

Krz: http://hostuje.net/file.php?id=01ef0e6572d9c3054826fb395d875666 mam nadzieje ze działa i mam nadzieje ze dadza punkty za rysunki

Eta: w zad. z ostrosłupem :

	2√2
sinα=
	3

liczyłam 2 razy

Patryks: Eta a jak oceniasz poziom tegorocznego rozszerzenia ?

Fr@nklin: 2011 trudny to pewnie i 2013 też będzie trudny...

xcvbnm: Tak się zastanawiam dlaczego na obecnym R nie ma praktycznie zadań z analizy funkcji? Żadnych optymalizacyjnych niczego, przecież to nie ma sensu w kontekście tego co robi się na studiach.