Odległość pkt od prostej SzymeQ: Mam pytanie, ile Wam wychodzi ta odległość, wyliczyłem środek okręgu jest ok., napisałem równanie prostej też jest dobrze teraz chcę obliczyć tą odległość i w odp jest co innego: S=(−1,3), r=5 prosta o równaniu w postaci ogólnej już ją przestawiłem: 2y+x−5=0

uhu: Jeśli chodzi ci o odl. środka od tej prostej, to wygląda na to że środek leży na tej prostej

SzymeQ: Nie odległość punktu od prostej, wzór: https://matematykaszkolna.pl/strona/1249.html

uhu: Ale jedynym pkt jaki podałeś jest środek

SzymeQ: nie podałem też równanie funkcji liniowej w postaci ogólnej, taka jak ma być do wzoru

uhu: podałeś > 2y+x−5=0

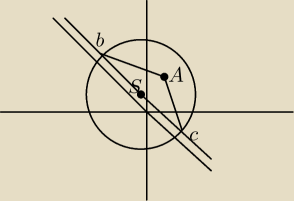
SzymeQ: no tak podstawiasz do wzoru najlepiej to narysować i wtedy wszystko widzisz. Mam takie zadanie. Oblicz pole trójkąta ABC, którego 1 z wierzchołków jest pkt A(2,5), a jednym z boków średnica okręgu x²+2x+y²−6y−15=0 równoległa do prostej x+2y=0 środek wyliczyłem jest dobrze tak jak w odpowiedziach Ta 1 od dołu to funkcja x+2y=0 >>> podana w treści Ta 2 to wyliczyłem i wzór 2y+x−5=0 >>> i to jest poprawnie chcę obliczyć wysokość czyli odległość pkt a od prostej 2y+x−5=0 >>> korzystam z wzoru co ci podałem wcześniej i wychodzi mi co innego niż w odpowiedzich

SzymeQ: bc to średnica czyli 2r=10 cm potrzebna mi wysokość obliczona z tego wzoru co pisałem wcześniej

uhu: x+2y−5=0 i pkt A(2,5)

	|2+10−5|
d=
	√5

SzymeQ: no kurde ja jak podstawiłem to co innego wyszło , a twoja odp się zgadza z odpowiedziami w książce. Muszę to przeanalizować, myślałem że błąd w książce.

asd: Jak wyliczyłeś prostą na której leży środek okręgu? Podstawiłeś punkt S(x,y) do wzoru na równanie okręgu? Jeżeli ta prosta ma taki wzór, jak napisałeś − to kolega podal dobry wzor

SzymeQ: a już wiem gdzie błąd nie uporządkowałem do końca postaci ogólnej i fanaberie podstawiałem dzięki wielkie

uhu: Zobacz może jako A brałeś współczynnik przy y zamiast przy x,

asd: d = ^{(1*2)+(2*5)−5}_(√1+√4

asd: zle sie zakodowalo. licznik: 1*2 + 2*5 − 5 w wartosci bezwzglednej mianownik: √1² + √2²

SzymeQ: ona jest równoległa do prostej x+2y=0 masz w treści zzadania to resztę obrałem środek jako punkt popodstawiałem i wyszło mi b czyli wyraz wolny bo reszta musi się zgadzać żeby były równoległe. Reszta to już spox łatwe, ta chwila nieuwagi może mnie zgubić na maturze

SzymeQ: "uhu: Zobacz może jako A brałeś współczynnik przy y zamiast przy x," właśnie tak uhu bo nie dokończyłem postaci ogólnej tylko poprzerzucałem na 1 stronę ale zapomniałem uporządkować dzięki

asd: S ( −1 , 3 ) I co? Bo napisałeś to dość niezrozumiale. Podstawiam sobie do wzoru y = ax + b dla a = −¹₂ 3 = ¹₂ + b no to b nie wychodzi 5?

SzymeQ: równanie x+2y=0, robię do postaci kierunkowej żeby je narysować, czyli y=−^x₂, czyli druga funkcja to y=−^x₂+b biorę środek okręgu jako punkt na prostej którą chcę obliczyć, podstawiam wychodzi b=2,5, teraz żeby się zgadzał wzór z pierwszą funkcją muszę pomnożyć *2 czyli y=−^x₂+2.5 ///*2 i wychodzi x+2y−5=0

SzymeQ: prościej się już nie da

asd: ale czemu musimy robic tak zeby wzor sie zgadzal z pierwsza? aby zachodzil warunek rownoleglosci prostych, to tak samo musza wartości wspolczynnikow kierunkowych wygladac?

SzymeQ: wszystkie wspólczynniki przy x i muszą się zgadzać, tu mam w postaci ogólnej, ale jak kierunkową masz to zawsze przemnażasz żeby po jednej stronie sam y został i wtedy porównujesz np w zadaniach testowych poziom podstawowy czy przy x jest to samo, to samo robię tutaj, chcę mieć to samo przy x. Po doprowadzeniu do postaci kierunkowej zauważ: y=−^x₂ >>> to jest wyjściowa funkcja, y=−^x₂+ 2,5 >>> to jest 2 funkcja w posatci kierunkowej, nie ma co tu dużo rozumieć

SzymeQ: https://matematykaszkolna.pl/strona/42.html tak wartości wsp. kierunkowych muszą się zgadzać, popatrz na link powyżej.