Oblicz długośc boków trójkąta Adrian: Długość jednej z przyprostokątnych trójkąta prostokątnego jest równa 3. Oblicz długości pozostałych boków tego trójkąta, jeśli: a) wysokość opuszczona na przeciwprostokątną jest równa √5 b) środkowa wychodząca z wierzchołka kąta prostego jest równa 2,5 Za rozwiązanie − z góry dziękuję

Nie jestem mądry: Za chwilkę rozwiążę

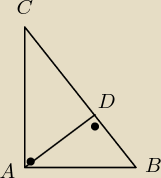
Nie jestem mądry: a) I AD I= √5 I AB I = 3 Trójkąt ABD : I DB I=x I DB I²=AB² − AD²= 9−5=4 ⇒ I DB I=2 Wzór na wysokość w trójkącie prostokątnym : h²= I CD I * I DB I zaznaczmy bok CB jako y wtedy CD= y−2 h²=2*(y−2) 5=2y−4 2y=9 ⇒ y= ⁹₂ Obliczamy bok AC z tw. Pitagorasa

	45		√45
AC2= (92)2− 9=		⇒ AC=
	4		2

Chyba nie pomyliłem się w obliczeniach

Nie jestem mądry: Z tą środkową jedyne co mi przychodzi do głowy to zastosować tw. cosinusów myślę że umiesz to zapisać i obliczyć

Adrian: Nic, a nic! Wszystkie obliczenia się zgadzają. Dziękuję za pomoc.

nie jestem mądra tym bardziej: Wzór na wysokość w trójkącie prostokątnym : h2= I CD I * I DB I że coo? o co chodzi z tym wzorem na wysokosć ? gubie sie w tym momencie.. co ja robie na rozszerzonej matmie..

ICSP: https://matematykaszkolna.pl/forum/206864.html − Eta ładnie wyprowadziła ten wzór

blah: środkowa kąta nie jest jego dwusieczną... środkowa kąta dzieli bok przeciwległy na dwa równe odcinki i wcale nie musi padać na dany bok prostopadle... zadanie jest zle zrobione