 Eta masz jakieś ambitniejsze zadanie na maturkę rozszerzoną, nie za bardzo mam
co robić
Eta masz jakieś ambitniejsze zadanie na maturkę rozszerzoną, nie za bardzo mam
co robić  ?
?


| 1 | ||
x = 3 | ||
| 4 |
| 2If(x)I | ||
b) Naszkicuj wykres funkcji g określonej wzorem g(x) = | ||
| f(x) |

 tutaj poniżej przykład:
zad1.
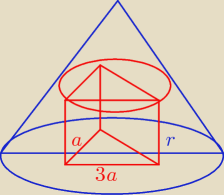
W stożek o promieniu r i kącie rozwarcia 2α wpisano rodzinę graniastosłupów prostych podstawy
dolne tych graniastosłupów zawierają się w podstawie stożka,a wierzchołki górnych podstaw
należą do powierzchni bocznej stożka . Podstawą każdego z graniastosłupów jest trójkąt
prostokątny w którym stosunek długości przyprostokątnych wynosi 3:1. Podaj wymiary tego z
graniastosłupów, który ma największą objętość.
mam napisać przepisać kilka innych?
tutaj poniżej przykład:
zad1.
W stożek o promieniu r i kącie rozwarcia 2α wpisano rodzinę graniastosłupów prostych podstawy
dolne tych graniastosłupów zawierają się w podstawie stożka,a wierzchołki górnych podstaw
należą do powierzchni bocznej stożka . Podstawą każdego z graniastosłupów jest trójkąt
prostokątny w którym stosunek długości przyprostokątnych wynosi 3:1. Podaj wymiary tego z
graniastosłupów, który ma największą objętość.
mam napisać przepisać kilka innych?




 Pokaż jakbyś zrobił
Pokaż jakbyś zrobił 
 ):
log2(4x−12)≥0
log2(4x−12)≥log21
4x−12≥1
4x≥13
x≥13/4 i mieści się ledwo z dziedziną x>3
log2(4x−12)<0
3<x<13/4
):
log2(4x−12)≥0
log2(4x−12)≥log21
4x−12≥1
4x≥13
x≥13/4 i mieści się ledwo z dziedziną x>3
log2(4x−12)<0
3<x<13/4
 https://matematykaszkolna.pl/forum/54574.html
Pozdrawiam.
https://matematykaszkolna.pl/forum/54574.html
Pozdrawiam.


 Sam liczę ten arkusz
Sam liczę ten arkusz 
 Czyli to ma być tak :
Czyli to ma być tak :
| 2If(x)I | ||
g(x) = | ||
| f(x) |
| 13 | ||
x > | ||
| 4 |
| 2f(x) | 13 | |||
g(x) = | = 2 dla x > | |||
| f(x) | 4 |
| 13 | ||
x < | ||
| 4 |
| 2[(−f(x)] | 13 | |||
g(x) = | = 2 dla x < | |||
| −f(x) | 4 |


| 2r(4 + √10) | 2r(4 + √10) | 4r(2√10 + 5) | ||||
Wymiary podstawy: | , | , | , | |||
| 9 | 3 | 9 |
| 1 | ||
Wysokość: | ctgα * r | |
| 3 |
 Czekam na potwierdzenie
Czekam na potwierdzenie  Przeciwprostokątna: √10a
R − promień opisanego na podstawie graniastosłupa:
H − wysokość stożka
h − wysokość graniastosłupa
Przeciwprostokątna: √10a
R − promień opisanego na podstawie graniastosłupa:
H − wysokość stożka
h − wysokość graniastosłupa
| H | ||
ctgα = | ||
| r |
| 4a − √10a | 4 − √10 | |||
R = | = | a | ||
| 2 | 2 |
| H | H − h | ||
= | |||
| r | R |
| 4 − √10 | ||
ctgα * r * | a = ctgα * r2 − r * h | |
| 2 |
| 4 − √10 | |
actgα = ctgα * r − h | |
| 2 |
| √10 − 4 | ||
h = ctgα * r + | actgα | |
| 2 |
| √10 − 4 | 3√10 − 12 | |||
V(a) = 3a2 * h = 3a2 − (ctgα * r + | actgα) = | a3ctgα + | ||
| 2 | 2 |
| 9√10 − 36 | ||
V'(a) = | a2ctgα + 6actgαr | |
| 2 |
| 9√10 − 36 | |
a2ctgα + 6actgαr = 0 /:3actgα | |
| 2 |
| 3√10 − 12 | |
a + 2r = 0 | |
| 2 |
| 4r | 4r(12 + 3√10) | 2r(4 + √10) | ||||
a = | = | = | ||||
| 12 − 3√10 | 144 − 90 | 9 |
| 2r(4 + √10) | 2r(4 + √10) | 4r(2√10 + 5) | ||||
Wymiary podstawy: | , | , | , | |||
| 9 | 3 | 9 |
| 1 | ||
Wysokość: | ctgα * r | |
| 3 |
 ?
?


| 2|f(x)| | ||
g(x) = | ||
| f(x) |
| 13 | ||
Gdy log2(4x − 12) > 0 ⇒ 4x − 12 > 1 ⇒ x > | ||
| 4 |
| 13 | ||
Gdy log2(4x − 12) < 0 ⇒ x < | ||
| 4 |
| ⎧ | 2 dla x ≥ 134 | ||
| g(x) = | ⎨ | ||
| ⎩ | −2 dla x ∊ (3,134) |
 już wiem skąd ta −2
już wiem skąd ta −2 









 Tylko boje się, że dadzą coś z prawdopodobieństwa ciężkiego
Tylko boje się, że dadzą coś z prawdopodobieństwa ciężkiego
 , a nie...
, a nie...




 oni tu dali coś takiego
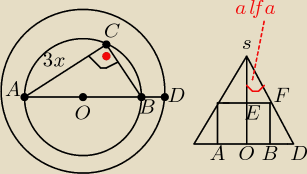
H−wysokość stożka, h−wysokość graniastosłupa, x− długość jednej przyprostokątnej,3x długość
drugiej. wtedy przyprostokątna ma długość x√10
Ponieważ trójkąt ABC jest prostokątny, więc przeciwprostokątna jest średnicą okręgu opisanego
na górnej podstawie graniastosłupa
Z trójkąta SOD : H=rctgα
oni tu dali coś takiego
H−wysokość stożka, h−wysokość graniastosłupa, x− długość jednej przyprostokątnej,3x długość
drugiej. wtedy przyprostokątna ma długość x√10
Ponieważ trójkąt ABC jest prostokątny, więc przeciwprostokątna jest średnicą okręgu opisanego
na górnej podstawie graniastosłupa
Z trójkąta SOD : H=rctgα
| 2(H−h) | ||
z Trójkąta SEF: | =ctgα | |
| x√10 |
| ctgα | ||
V(x)= | (−3√10x3+6rx2) | |
| 4 |
| 2r | ||
x∊(0, | ) | |
| √10 |
| ctgα | ||
V'(x)= | (−9√10x2+12rx) | |
| 4 |
| 2r | ||
x∊(0, | ) | |
| √10 |
| 4r | ||
V'(x)=0 dla x= | ||
| 3√10 |
| π | ||
ponieważ α∊(0, | ), więc ctgα>0 | |
| 2 |
| 4r | ||
V'(x)>0 dla x∊(0, | ) | |
| 3√10 |
| 4r | 2r | |||
V'(x)>0 dla x∊(x, | , | ) | ||
| 3√10 | √10 |
| 2r | ||
x→ | V(x)=0, | |
| √10 |
| 4r | ||
stąd objętość graniastosłupa jest największa gdy x= | ||
| 3√10 |
| 4r | 4 | rctgα | ||||
wtedy 3x= | ,√10*x= | r, h= | ||||
| √10 | 3 | 3 |
| 4r | 4r | 4 | ||||
odp: Krawędzie podstawy mają długości | , | , | r, zaś krawędz boczna | |||
| 3√10 | √10 | 3 |
| rctgα | ||
ma długość | ||
| 3 |

| √10a | ||
z promieniem okręgu wpisanego, R = | ||
| 2 |
 Jak chcesz to zeskanuje coś jeszcze z tego zbioru,
to dawne zadanka z podstawy programowej. Tak je oglądam i się zastanawiam.. ciekawe co by
powiedzieli humaniści co narzekają że obecna matma w liceum jest trudna jakby przywrócili
stary program z lat 80 i matura była by obowiązkowa jak teraz
Jak chcesz to zeskanuje coś jeszcze z tego zbioru,
to dawne zadanka z podstawy programowej. Tak je oglądam i się zastanawiam.. ciekawe co by
powiedzieli humaniści co narzekają że obecna matma w liceum jest trudna jakby przywrócili
stary program z lat 80 i matura była by obowiązkowa jak teraz 



 belzebub@
dokładnie , fajnie mieli 5 godzin aż z czego tylko 3 musieli zrobić na bdb.
belzebub@
dokładnie , fajnie mieli 5 godzin aż z czego tylko 3 musieli zrobić na bdb.