Horsemen: Na okręgu o równaniu x ²+y ²=1 wyznacz taki punkt M=(x,y), aby wyrażenie 3x+4y miało jak największą wartość. Bardzo prosiłbym o szybką odpowiedź, jakieś wskazówki - jakby się dało to jeszcze dzisiaj. Z góry dziękuję.

b.: Można np. tak: punkty okręgu spełniają y = √1-x² lub y= - √1-x². Ten drugi przypadek można pominąć, bo dla y=√1-x² otrzymamy zawsze >= wartość wyrażenia 3x+4y niż dla y=-√1-x². Czyli maksymalizujemy wyrażenie 3x+√1-x² dla x z przedziału [-1,1], to można zrobić licząc pochodną... 387

b.: Można też tak, chociaż nie wiem, czy tak się robi w liceum chodzi o maksymalizację wyrażenia 3x+4y = (3,4) o (x,y) (iloczyn skalarny wektorów (3,4) i (x,y)) Mamy (3,4) o (x,y) = | (3,4)| * |(x,y)| * cos α = = 5 * √x²+y² * cos α = = 5 cos α gdzie α jest kątem między wektorami (3,4) i (x,y). Największą wartość dostaniemy, gdy α=0, czyli gdy wektory są równoległe i mają taki sam zwrot, tzn. (x,y) = β(3,4) dla pewnej β>=0. Ponieważ x²+y² =1, dostajemy stąd 9β² + 16β² = 1, czyli β=1/5, czyli x=3/5, y=4/5, a max wartość wyrażenia to 5.

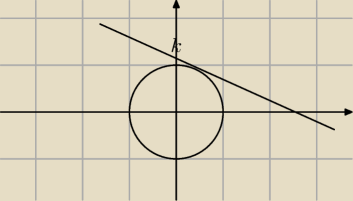
Nuk: Interpretacja geometryczna, bez pochodnych i wektorów, jedynie obliczenia odrobinę czasochłonne 3x+4y=k, gdzie k to największa suma. Stąd: y=−³₄x+^k₄ Szukamy więc prostej równoległej do y=−u{3/4} stycznej do okręgu opisanego w zadaniu, o jak największym k. Po podstawieniu do równania okręgu i zażądaniu Δ=0 otrzymujemy k=5 ∨ k=−5. Odrzucamy drugi przypadek, gdyż k ma być jak najwieksze. Dla k=5 otrzymujemy x=³₅, y=⁴₅, współrzędne szukanego punktu M.