trapez ania.m.: trapez równoramienny o podstawach 10 i 20 cm i ramionach 13 cm obraca się dookoła−dłuższej podstawy i krótszej podstawy.oblicz objętość i pole powierzchni całkowitej otrzymanych brył.

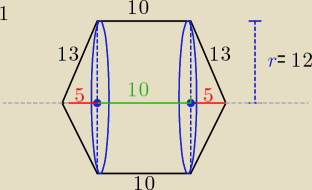
Eta: 1/ obrót trapezu dookoła dłuższej podstawy Powstała bryła składa się z walca z naklejonymi na jego podstawy stożkami o tej samej objętości H(walca)= 10 , h( stożka) = 5 , tworząca stożka l= 13 z tw. Pitagorasa: r²= 13² −5²= 144 to: r(podstawy walca i stozka)= 12 V( bryły) = V( walca) + 2*V( stozka) =........ podstaw dane i dokończ obliczenia P_c( bryły)= P_b( walca) + 2*P_b( stożka) =.............. dokończ bo pole liczymy tak jakbyś tę bryłę malowała farbą, czyli tylko po powierzchniach bocznych ( bo stozki i walec są sklejone )

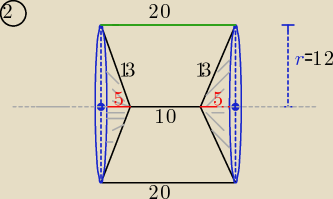
Eta: 2/ to bryła powstała z obrotu trapezu dookoła krótszej podstawy składa się z walca i wydrążonych z obydwu stron stożków o tej samej objetości wymiary: H( walca) = 20 , h(stozków )= 5 l= 13 i r= 12 V bryły = V( walca − 2*V( stożka)=............... znów wyobraź sobie malownie tej bryły) zatem: P_c( bryły)= P_b( walca + 2*p_b ( stozka)= ............ teraz tylko podstaw do wzorów i ..........dokończ obliczenia