Bryły Dawid: Oblicz objętość i pole powierzchni całkowitej stożka otrzymanego w wyniku obrotu a)Trójkąta prostokątnego o przyprostokątnych 3 i 6 cm wokół krótszej przyprostokątnej, b)Trójkąta równobocznego o obwodzie 12cm wokół wysokości

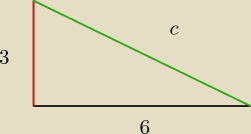
:P: a).to jest trójkąt prostokątny taki jak mamy w zadaniu a) możemy policzyć długość przeciwprostokątnej z twierdzenia pitagorasa. c² = 3²+6² c² = 45 c = 3√5 i teraz obracamy wokół krótszej przyprostokątnej, (tej na czerwono) i powstaje ... ciąg dalszy niżej

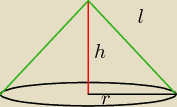
:P: teraz widzimy, że czarna kreska to będzie r, czyli r = 6 wysokość na czerwono, więc h = 3 wzór na objętość stożka jest taki: −−−−> V = ¹₃πr²*h ,, mamy wszystko tylko podstawić V = ¹₃*36π*3 = 36π [cm³] Pole całkowite = 2πr + πrl, tyle że w tym przypadku l=c, które policzyliśmy wcześniej, czyli Pole całkowite = 2πr + πrc Pole całkowite = 2π6 + π6*3√5 = 12π + 18√5π = 6π (2 + 3√5).

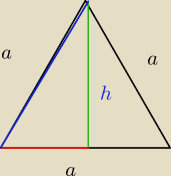
:P: b). Owb = 12cm = a+a+a = 3a 3a = 12 a = 4 wzór na wysokość trójkąta równobocznego −−−> 856 h = ^a√3₂ h = ^4√3₂ = 2√3 obracamy wokoło wysokości, (zielona)

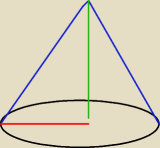
:P: sorki, troche krzywy rysunek ^^ h mamy h = 2√3 r = ¹₂a (połowa "a", czyli połowa boku trójkąta równobocznego, czerwonej kreski) a = 4 r = 2 l = 4 <−−− bok trójkąta równobocznego V = ¹₃*πr²*h = ¹₃π2²*2√3 = ^8√3π₃ Pole całkowite = 2πr + πrl = 2*2π + π2*4 = 4π + 8π = 12π