Znajdz miejsce zerowe wielomianow qń: Znajdź miejsce zerowe i wyprowadź postać iloczynową: a) (x² − 2x)² − 1 = 0 b) x³ − x² = −5 − 3x c) (x+1)(x+√5) = 0

:P: a) (x² − 2x)² − 1 = 0 x⁴ − 4x³ + 4x² − 1 = 0 dla x=1 1 −4 +4 −1 = 0 czyli "1" jest pierwiastkiem równania schemat chornera 1401 rysunek czyli mamy teraz wzór x³ −3x² + x + 1 = 0 znowu x = 1 będzie pasowało 1−3+1+1 = 0 czyli "1" jest pierwiastkiem II rzędu następny schemat niżej

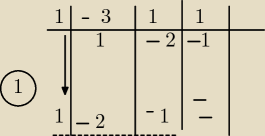
:P: i mamy wzór z tego co zostało podkreślone przerywaną, czyli x² − 2x − 1 = 0 Δ = 4 + 4 = 8 √Δ = √8 x₂ = ^{2 − √8}₂ = 1 − ^√8₂ x₃ = ^{2 + √8}₂ i to co było wcześniej x₁ = 1 <−−−− (pierwiastek II rzędu) ale nie przepisuj tego to jest źle prawdopodobni, jakby mógł ktoś sprawdzić

:P: x³ − x² + 3x + 5 = 0 dla x = −1 mamy −−−> −1 −1 −3 +5 = 0 <−−−− zgadza się "−1" jest pierwiastkiem mamy x² −2x +5 = 0 Δ = 4−20 <0, czyli nie ma tutaj pierwiastków, czyli jedyny pierwiastek funkcji x³ − x² + 3x + 5 = 0 to x = −1 (x² −2x +5) (x+1) = 0

:P: c). postać iloczynowa już jest, czyli miejsca zerowe. x+1=0 czyli x = −1 oraz x+√5 = 0, czyli x = −√5 miejsca zerowe −−−> {−√5, −1) zadanie a) jest prawdopodobnie źle