a sms: Oblicz długość promienia okręgu wpisanego w trójkąt prostokątny równoramienny, którego przeciwprostokątna ma długość 4 cm Jest takie rozwiązanie: r=2P/(a+b+c) P=1/2ah h=b=a a=4 cm P=1/2a² P=1/2*4² P=8 cm² 4²+4²=c² c²=16+16 c²=32 c=√32 c=4√2 r=2*8/(4²*4√2) r=16/(16*4√2) r=1/4√2 r=√2/8 1)Czy zamiast tego wzoru: r=2P/(a+b+c) mógłby być ten: r=a+a−c/2 2)Czy to zadanie jest dobrze zrobione?

sms: prosze o pomoc

sms: ....

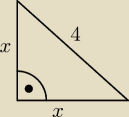
Tragos: z tw. Pitagorasa x² + x² = 4² 2x² = 16 x² = 8 x = √8 = 2√2

	1		1
P =		*x*x =		*8 = 4
	2		2

P = pr

	P
r =
	p

	x+x+4		2√2 + 2√2 + 4
p =		=		= 2√2 + 2
	2		2

	4		4		2		√2 − 1
r =		=		=		*		= 2√2 − 2
	2√2 + 2		2(√2 + 1)		√2 + 1		√2 − 1

sms: napisz co to jest to p i P i czemu tam jest wzór P=pr i r=P/p

sms: proszę o odpowiedź. chce coś wiedzieć z tego zadania a nie tylko bezmyślnie przepisać i dostać 1

Tragos: P to pole a p to połowa obwodu jest taki wzór P = pr https://matematykaszkolna.pl/strona/542.html tutaj jest ten wzór, tylko w innej formie, on wychodzi z tego, który podałem wyżej