Parametr funkcji malejącej i liczby spełniające warunek. Lelon3: Witam. Mam dwa zadanka do ogarnięcia. 1. Dla jakiego parametru funkcja liniowa f(x) = (2m−4)x+3 jest malejąca? 2.Na osi liczbowej zaznacz liczby spełniające warunek lxl ≥ 1. Powtarzamy do matury (mimo iż za rok dopiero) i już nie bardzo pamiętam jak się to obliczało. Będę ogromnie wdzięczny za pomoc i objaśnienia.

dero2005: 1) funkca liniowa jest malejąca gdy a<0 czyli 2m−4<0 2m<4 m<2

Lelon3: Acha, więc to tak szło. Dzięki wielkie!

Lelon3: Jeszcze tylko potrzebuje tego drugiego. Tam wystarczy zaznaczyć od +1 w prawo z zamalowanym kółkiem? Czy coś trzeba z wartością bezwzględną kombinować?

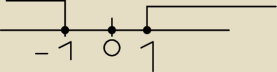
ceaser I: x∊(−∞−1≥ U ≤1,+∞)

sadadsa: siemanko, 1) żeby funkcja liniowa była malejąca to liczba przy "x" musi być mniejsza od 0. my mamy przy "x" (2m−4) i to musi być mniejsze od 0. Gdyby to było równe 0 to funkcja byłaby stała i wynosiłaby y=3, a gdy 2m−4 jest większe od 0 to funkcja rosnąca. Poczytaj więcej jeszcze tutaj. 41 czyli my mamy 2m−4<0 2m<4 m<2 m∊(−∞, 2) 2) to podobne zadanie to tego −−−> 1098 czyli mamy coś takiego |x| ≥ 1 x ≥ 1 i x ≤ −1 <−−−−ja to się tak uczyłem rozwiązywać, pierwsz przpisujesz normalnie, a później odwracasz znak nierówności i zmieniasz liczbe na przeciwną. 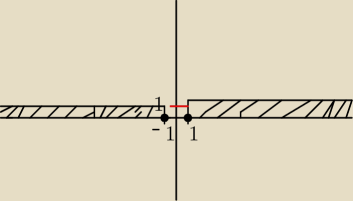i z tego wychodzi nam, że x∊ (−∞, −1> ∪ <1, +∞) i do tego rysunek. pamiętaj o tych kropkach, tam gdzie −1 i 1 one są ważne bo przedziały są domknięte. a ta kreseczka, na czerwono, to ma jej nibyć (błąd ^^ ). pozdrawiam, jak coś pytaj.

Lelon3: Teraz już czaję. Dzięki!

ceaser I: sadadsa proste przykłady chyba łatwiej jest graficznie rozwiązywać przynajmniej dla mnie