graniastosłupy Kaś: Pole podstawy prostopadłościanu to 12 cm *2 .przekątna prostopadłościanu jest równa 5 pierwiastków z 2. długość podstawy jest o 1 większa od szerokości podstawy. oblicz długość przekątnych ścian bocznych dryły

ICSP: krótszy bok z podstawie − x dłuższy bok w podstawie − x+ 1 Pole podstawy − 12 x(x+1) = 12 x² + x − 12 = 0 ⇔ x = 3 v x = − 4 . x = − 4 jest sprzeczne wiec zostaje 3 długość podstawy: 3 , 4 wzór na przekątną: d = √a² + b² + c² gdzie a i b są długościami boków w podstawie a c wysokością tego prostopadłościanu 5√2 = √9 + 16 + c² ⇔ 50 = 25 + c² ⇔ c = 5 v c = − 5. Tak samo − 5 jest sprzeczne. przekątne ścian bocznych obliczysz już sam/a z twierdzenia pitagorasa.

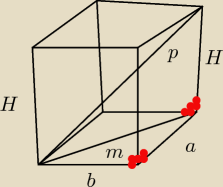
asd: a −− jeden bok podstawy (dajmy, że długość) b −− drugi bok podstawy (więc to jest szerokość) p − przekątna prostopadłościany P_p −−− pole podstawy m −− przekątna podstawy H −− wysokość prostopadłościanu na rysunku pozaznaczane b>0 i a>0 "b" i "a" muszą byc większe od 0 bo to długości boków. to jest założenie p = 5√2 P_p = 12 a = b + 1 SZUKANE x −− przekątna ściant = ? y −−− przekątna innej ściany = ? ten prostopadłościan ma 2 różne pary ścian wiemy, że P_p to a*b (bo to jest prostokąt), czyli a*b = 12 a = b + 1 −−−−−−> mamy taki układ równań podstawiamy a (b + 1)b = 12 b² + b −12 = 0 <−−−− równanie kwadratowe 54 Δ = 1 + 48 = 49 √Δ = 7 b₁ = ^{−1 −7}₂ = i{−8}{2} = −4 b₂ = ⁻¹⁺⁷₇ = ⁶₂ = 3 b>0 więc zostaje tylko b=3 a = b+1 = 3+1=4 a=4 b=3 tam gdzie na czerwono sa kąty proste (na rysunku może tego nie być widać) teraz chcemy policzyć H (wysokość prostopadłościanu) ale musimy na początek musimy policzyć "m" czyli przekątną podstawy m² − a² + b² <−−−−−−twierdzenie pitagorasa m² = 16+9 = 25 m = √25 = 5 <−−− mamy "m" więc m² + H² = p² <−−−−−− znowu twierdzenie itagorasa H² = p² − m² H² = (5√2)² − 5² = 50 − 25 = 25 H = √25 = 5 teraz wyobraź sobie sciana boczna to prostokąt o bokach b i H lub a i H, czyli 3 i 5 lub 4 i 5 czyli przekątną tej ściany bocznej też możemy z pitagorasa obliczyć dla x −−−−> x² = a² + H² x² = 16+25 = 41 x = √41 dla y −−−−> y² = b² + H² y² = 9+25 = 34 y = √34 Odp: x=√41 i y = √34 przeanalizuj to sobie zeby zapamiętać jak coś to pytaj