Matura
(d()b): Wyznacz wszystkie wartości parametru m, m ∊ R, dla których równanie | x − 4| − x = m
ma tylko jedno rozwązanie.
24 lut 12:17
(d()b): pomocy

24 lut 12:27
(d()b): pomoże ktoś?
24 lut 12:35
(d()b): Poprawka: | | x − 4| − x| = m

24 lut 12:40
(d()b):
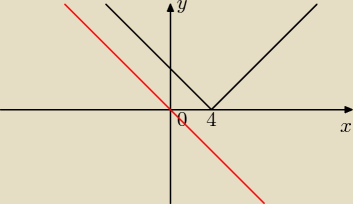
Teoretycznie rozwiązałbym to:
|x − 4| − x = 0
|x − 4| = x
Wykres powyżej ale wątpie czy to dobrze jest

24 lut 12:43
Bogdan:
Wykres y = x + m (czerwony) jest źle narysowany
24 lut 12:53
(d()b): A jak powinien być?
24 lut 12:56
24 lut 13:00
(d()b): no właśnie dlatego narysowałem y = x
24 lut 13:02
(d()b):
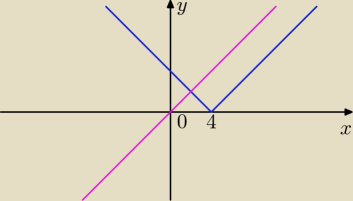
Tak o

?
i m∊(−
∞;0)
24 lut 13:04
Bogdan:
Tak, to jest wykres y = x + m dla m = 0.
Znajdź wszystkie wartości m spełniające warunki zadania.
24 lut 13:09
(d()b): no właśnie warunki zadania − 1 rozwiązanie
więc chyba m∊(−∞; 0)
24 lut 13:13
(d()b): halo

24 lut 13:22
(d()b): halo
24 lut 13:55
Ukasz: Ja bym to zrobił tak:
|x−4|−x=m
−x+4−x−m=0 v x−4−x−m=0
,ale mogę się mylić.
24 lut 14:06
Bogdan:
Widać, że prosta y = x + m przecina wykres y = |x − 4| dla m > −4, czyli m∊(−4, +∞).
Dla m = −4 jest nieskończenie wiele rozwiązań, dla m < −4 nie ma rozwiązań.
24 lut 14:21
(d()b): czyli jaka powinna być odpowiedź

?
24 lut 14:59
(d()b): jaka poprawna odpowiedź

?
24 lut 15:31


 Teoretycznie rozwiązałbym to:
|x − 4| − x = 0
|x − 4| = x
Wykres powyżej ale wątpie czy to dobrze jest
Teoretycznie rozwiązałbym to:
|x − 4| − x = 0
|x − 4| = x
Wykres powyżej ale wątpie czy to dobrze jest
 Tak o
Tak o  ?
i m∊(−∞;0)
?
i m∊(−∞;0)

 ?
?
 ?
?