Sterometria - POMOCY!!! Volde: Witam. Proszę o pomoc w zadaniach ze graniastosłupów, ostrosłupów: 5.Dany jest ostrosłup prawidłowy trójkątny, którego wysokość wynosi 8 cm i tworzy z płaszczyzną ściany bocznej kąt "alfa" taki, że, sin "alfa"=3/5. Oblicz pole powierzchni całkowitej i objętość bryły. 6..Dany jest ostrosłup prawidłowy trójkątny, którego wysokość ściany bocznej o mierze 10 cm tworzy z płaszczyzną podstawy kąt "alfa" taki, że, sin "alfa"=4/5. Oblicz pole powierzchni całkowitej i objętość bryły. W zadaniach 5, 6 prosiłbym o zamieszczenie rysunków. Z poważaniem. Łukasz Nowakowski.

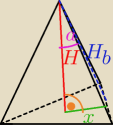
patryk: skoro ostrosłup prawidłowy, w podstawie jest trójkąt równoboczny.

	x		3Hb
jak z rysunku widać, sin α =		⇒ x =
	Hb		5

	9Hb2
z twierdzenia Pitagorasa: Hb2 = H2 + x2 ⇒ Hb2 = 82 +
	25

mnożymy obustronnie przez 25 25H_b² = 25*64 + 9H_b² 16H_b² = 25*64 H_b² = 25*4 ⇒ H_b = 10 a z tego wynika, że x = 30:5 = 6 cm własności trójkąta: https://matematykaszkolna.pl/strona/856.html Z własności wiemy, że środek trójkąta będzie w przecięciach się

	h		h
wysokości (równoboczny jest) a to jest		więc		= 6 cm, ze wzorów wiemy, że h =
	3		3

	a√3
		, podstawiamy
	2

a√3
	= 6
6

	√3*36
a√3 = 36 ⇒ a =		= 12√3
	3

	a2√3
Pp =
	4

	Pp*H
V =		, masz objętość,
	3

P_c = P_p + 3P_b

	a*Hb
a Pb =
	2

drugie analogicznie