wielomiany iwa: Dany jest wielomian W(x)=x³+2x²−9x−18 a) wyznacz pierwiastki tego wielomianu b) sprawdź, czy wielomiany W(x) i P(x) = (x+2)(x²−2x+4)+(x+2)(2x−13) są równe

iwa: Proszę o pomoc!

asd: W(x)=x³ + 2x² − 9x − 18 = x(x² − 9) + 2(x² − 9) = <−−−−−zauważ, że w nawiasie jest to samo = (x² − 9) (x + 2) = <−−−− to pierwsze to wzór skróconego mnożenia 55 = (x−3) (x+3) (x+2) = 0 czyli mamy x=3 i x=−3 i x=−2 p(x)=x³ − 2x² + 4x + 2x² − 4x + 8 +2x² − 13x + 4x −26 <−−wymnożone i po zredukowaniu mamy P(x) = x³ + 2x² − 9x −18 = W(x) czyli są sobie równe.

Noah: x³+2x²−9x−18=0 x²(x+2)−9(x+2)=0 (x²−9)(x+2)=0 (x−3)(x+3)(x+2)=0 x−3=0 v x+3=0 v x+2=0 x=3 v x=−3 v x=−2 x∊{−3,−2,3} b) wymnoz i dodaj wyrazy podobne w wielomianie P(x) i sprawdz czy jest taki sam jak wielomian W(X)

asd: ważne żebyś rozumiała o co chodzi jak coś nie jasne to pytaj co

iwa: Ok bardzo dziękuję wszystko jasne tylko jeszcze jedno uzasadnij, ze jeśli x>√10, to x³+2x²−9x−18>0

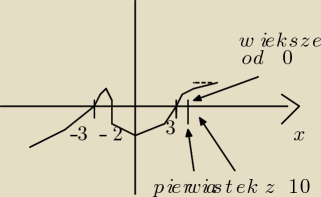
asd: w podobny sposób. x(x² − 9) + 2(x² − 9) >0 (x² − 9) (x+2) >0 (x−3) (x+3) (x+2) >0 x=3 i x=−3 i x=−2 zaczynamy wykres rysować od góry, bo nie ma minusu przed x³ wszystkie pierwiastki są jednowartościowe, więc nie odbijamy nic od osi "x" zobacz tutaj 142 i odczytujemy co jest ponad osią x x∊(−3, −2) ∪ (3, +∞) zauważ, że √10 >3 więc jeśli jest √10 to funka jest większa od "0"

iwa: Wszystko jasne dziękuję